练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

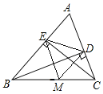
    【题目】如图,已知BD、CE是△ABC的高,M是BC边上的中点,若△EMD是等腰直角三角形,则∠A=________°

    【答案】45

    【解析】

    首先根据直角三角形斜边上的中线等于斜边的一半，得出BM=EM=CM=DM，进而得出∠ABC=∠BEM，∠ACB=∠CDM，又根据△EMD是等腰直角三角形,得出∠EMD=90°，通过等量转换，即可得出∠A.

    ∵BD、CE是△ABC的高,M是BC边上的中点,

    ∴BM=EM=CM=DM，

    ∴∠ABC=∠BEM，∠ACB=∠CDM，

    又∵△EMD是等腰直角三角形,

    ∴∠EMD=90°

    ∴∠BME+∠CMD=90°=（180°-2∠ABC）+（180°-2∠ACB）=360°-2（180°-∠A）

    ∴∠A=45°

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】小明同学在学习与圆有关的角时了解到：在同圆或等圆中，同弧（或等弧）所对的圆周角相等．如图，点A、B、C、D均为⊙O上的点，则有∠C=∠D．

    小明还发现，若点E在⊙O外，且与点D在直线AB同侧，则有∠D >∠E． 请你参考小明得出的结论，解答下列问题：

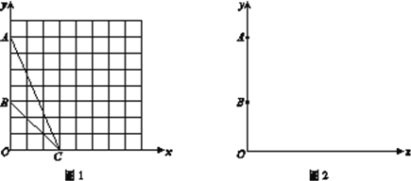
    （1）如图1，在平面直角坐标系xOy中，点A的坐标为(0,7)，点B的坐标为(0,3)，点C的坐标为(3,0) ．①在图1中作出△ABC的外接圆（保留必要的作图痕迹，不写作法）；

    ②若在轴的正半轴上有一点D，且∠ACB =∠ADB，则点D的坐标为________；

    (2) 如图2，在平面直角坐标系xOy中，点A的坐标为(0,m)，点B的坐标为(0,n)，其中m>n>0．点P为轴正半轴上的一个动点，当∠APB达到最大时，直接写出此时点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC，AB=AC，AC的垂直平分线与AB所在直线相交所得的锐角为40°，∠C=______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y=﹣x2+bx+c与一直线相交于A（﹣1，0）、C（2，3）两点，与y轴交于点N，其顶点为D．

    （1）求抛物线及直线AC的函数关系式；

    （2）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值及此时点P的坐标；

    （3）设点M（3，n），求使MN+MD取最小值时n的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】从﹣2，﹣1，0，1，2，3，4这7个数中任选一个数作为a的值，则使得关于x的分式方程有整数解，且关于x的一次函数y=（a+1）x+a﹣4的图象不经过第二象限的概率是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰直角△ABC中，∠ACB=90°，CA=CB，CD为斜边AB上的中线．

    （1）如图1，AE平分∠CAB交BC于E，交CD于F，若DF=2，求AC的长；

    （2）将图1中的△ADC绕点D顺时针旋转一定角度得到△ADN，如图2，P，Q分别为线段AN，BC的中点，连接AC，BN，PQ，求证：BN=PQ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将以直角顶点为旋转中心顺时针旋转，使点刚好落在上（即：点），若，则图中

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将边长为1的小正方形拼成一行一字排开，A1、A2、A3…依次是第2、3、4…个小正方形右下角的顶点，P是第一个小正方形左上角的顶点．记△PA1A2、△PA1A3，△PA1A4…依次为①号三角形、②号三角形、③号三角形…．已知这些三角形中有一个三角形与①号三角形相似，则这个三角形的号数为（　　）

    A. ③ B. ④ C. ⑤ D. ⑥

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1）所示为一个无盖的正方体纸盒，现将其展开成平面图，如图(2)所示．已知展开图中每个正方形的边长为1：

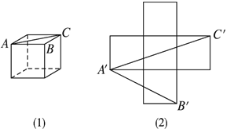
    (1)在展开图(2)中可画出最长线段的长度为 ，在平面展开图(2)中这样的最长线段一共能画出 条。

    (2)试比较立体图中∠ABC与平面展开图中∠A′B′C′的大小关系，并说明理由。

    查看答案和解析>>

    同步练习册答案