
【题目】如图,将![]() 以直角顶点
以直角顶点![]() 为旋转中心顺时针旋转,使点
为旋转中心顺时针旋转,使点![]() 刚好落在
刚好落在![]() 上(即:点
上(即:点![]() ),若
),若![]() ,则图中
,则图中![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
先利用互余计算出∠B=35°,再根据旋转的性质得CA=CA′,∠ACA′=∠BCB′,∠B′=∠B=35°,则利用等腰三角形的性质得∠CA′A=∠CAA′=55°,于是利用三角形内角和可计算出∠ACA′=70°,则∠BCB′=70°,然后根据三角形外角性质计算∠1的度数.
在Rt△ABC中,∠B==90°∠A=35°,
∵Rt△ABC以直角顶点C为旋转中心顺时针旋转,使点A刚好落在AB上(即:点A′),
∴CA=CA′,∠ACA′=∠BCB′,∠B′=∠B=35°,
∴∠CA′A=∠CAA′=55°,
∴∠ACA′==180°2×55°=70°,
∴∠BCB′=70°,
∴∠1=∠BCB′+∠B′=70°+35°==105°.
故选C.


科目:初中数学 来源: 题型:
【题目】我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线![]() 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:

(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周的某一天,小王全家上午8时自驾小汽车从家里出发,到“番茄农庄”游玩,小汽车离家的距离![]() (千米)与小汽车离家后时间
(千米)与小汽车离家后时间![]() (时)的关系可以用图中的折线表示,根据图像提供的有关信息,解答下列问题:
(时)的关系可以用图中的折线表示,根据图像提供的有关信息,解答下列问题:

(1)“番茄农庄”离家________千米;
(2)小王全家在“番茄农庄”游玩了________小时;
(3)去时小汽车的平均速度是________千米/小时;
(4)回家时小汽车的平均速度是________千米/小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC, ∠A=40°,O为边BC的中点,把△ABC绕O顺时针旋转m(0<m<180)度后,如果点B恰好落在初始△ABC的边上,那么m=_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),Rt△AOB中,∠A=90°,∠AOB=60°,OB=![]() ,∠AOB的平分线OC交AB于C,过O点做与OB垂直的直线ON.动点P从点B出发沿折线BC﹣CO以每秒1个单位长度的速度向终点O运动,运动时间为t秒,同时动点Q从点C出发沿折线CO﹣ON以相同的速度运动,当点P到达点O时P、Q同时停止运动.
,∠AOB的平分线OC交AB于C,过O点做与OB垂直的直线ON.动点P从点B出发沿折线BC﹣CO以每秒1个单位长度的速度向终点O运动,运动时间为t秒,同时动点Q从点C出发沿折线CO﹣ON以相同的速度运动,当点P到达点O时P、Q同时停止运动.
(1)求OC、BC的长;
(2)设△CPQ的面积为S,求S与t的函数关系式;
(3)当P在OC上Q在ON上运动时,如图(2),设PQ与OA交于点M,当t为何值时,△OPM为等腰三角形?求出所有满足条件的t值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图
如图![]() ,线段
,线段![]() ,
,![]() ,点
,点![]() 从点
从点![]() 开始绕着点
开始绕着点![]() 以
以![]() 的速度顺时针旋转一周回到点
的速度顺时针旋转一周回到点![]() 后停止,点
后停止,点![]() 同时出发沿射线
同时出发沿射线![]() 自
自![]() 点向
点向![]() 点运动,若点
点运动,若点![]() 、
、![]() 两点能恰好相遇,则点
两点能恰好相遇,则点![]() 运动的速度为________
运动的速度为________![]() ;
;

![]() 将一副三角板中的两块直角三角尺的直角顶点
将一副三角板中的两块直角三角尺的直角顶点![]() 按如图方式叠放在一起(其中,
按如图方式叠放在一起(其中,![]() ,
,![]() ,
,![]() ;
;![]() ).将三角尺
).将三角尺![]() 固定,另一三角尺
固定,另一三角尺![]() 的
的![]() 边从
边从![]() 边开始绕点
边开始绕点![]() 转动,转动速度与
转动,转动速度与![]() 问中
问中![]() 点速度相同,当
点速度相同,当![]() 且点
且点![]() 在直线
在直线![]() 的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出
的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出![]() 有可能的值及对应转动的时间;若不存在,请说明理由.
有可能的值及对应转动的时间;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(1,a)在抛物线y=x2上.
(1)求A点的坐标;
(2)在x轴上是否存在点P,使得△OAP是等腰三角形?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
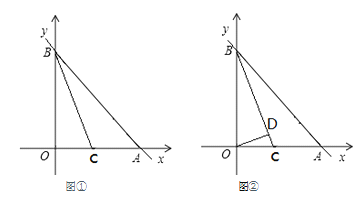
【题目】如图①,直线AB与x轴正半轴交于A(a,0)与y轴正半轴交于B(0,b).
(1)若a+b=8,且![]() ,求△AOB的面积;
,求△AOB的面积;
(2)若分式![]() 的值为0,过点B作BC平分∠OBA交x轴于C点,求证:
的值为0,过点B作BC平分∠OBA交x轴于C点,求证:![]() ;
;
(3)如图②,在(2)的条件下,过O点作OD⊥BC于D点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com