
����Ŀ����֪����ͼ���ڡ�ABC�У���B=90�㣬��A=30�㣬BC=5cm������Rt��DEF�У���FDE=![]() ��DE=3cm������D��Eʼ���ڱ�AB�ϣ�����D��A����AC�����ƶ���
��DE=3cm������D��Eʼ���ڱ�AB�ϣ�����D��A����AC�����ƶ���
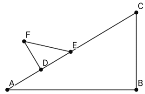
��1����Rt��DEF��AC�����ƶ��Ĺ����У�F��C����֮��ľ�����_______��������䡰���С����
��2����F��C������ABƽ��ʱ����AD�ij���
��3�����߶�AD��FC��BC�ij���Ϊ���߳�����������ֱ��������ʱ����AD�ij�
���𰸡���1����С����2��![]() ;��3��AD=6.7cm��4.2cm.
;��3��AD=6.7cm��4.2cm.
��������
��1�����������֪��DF=3cm��DC��С���ٸ��ݹ��ɶ��������жϣ�
��2������30�����Ե�ֱ�DZ���б�ߵ�һ���ƽ���ߵ����ʣ��ɵã�AC=2BC=10cm����FCD=��A=30�㣬�ٸ���������Ǻ������CD���Ӷ����AD��
��3����AD=x�����������֪��0��x��10��3=7����CD= AC��AD=10��x���ٸ��ݹ��ɶ����ɵã�FC=![]() ��Ȼ�����ֱ��������б�ߵ�����������ۣ�������ù��ɶ����ֱ����ÿ�������x��ֵ����.
��Ȼ�����ֱ��������б�ߵ�����������ۣ�������ù��ɶ����ֱ����ÿ�������x��ֵ����.
�⣺��1�����������֪��DF=DE=3cm��DC��С��
���ݹ��ɶ����ɵã�FC=![]()
��F��C����֮��ľ�����С��
�ʴ�Ϊ����С��
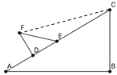
��2������ͼ��ʾ��FC��AB
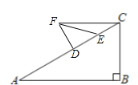
�ߡ�B=90�㣬��A=30�㣬BC=5cm��
��AC=2BC=10cm����FCD=��A=30��
��Rt��CFD��CD=![]() cm
cm
��AD=AC��CD=![]() ��
��
��3����AD=x�����������֪��0��x��10��3=7����CD= AC��AD=10��x
���ݹ��ɶ����ɵã�FC=![]()
����ADΪб��ʱ��
��AD2=FC2+BC2
��![]()
��ã�![]() ��
��
����FCΪб��ʱ��
��FC2= AD2 +BC2
��![]()
��ã�![]() ��
��
����BCΪб��ʱ��
��BC2= AD2 + FC2
��![]()
�����ã�![]()
��![]()
��˷�����.
����������AD=6.7cm��4.2cm.


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD��AF�۵���ʹ��D����BC�ߵĵ�E��������E��EG��CD��AF�ڵ�G������DG��
(1)��֤���ı���EFDG�����Σ�
(2)����DE����AF��O�㣬��̽���߶�EG��GF��AF֮���������ϵ����˵�����ɡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͬѧ��ѧϰ��Բ�йصĽ�ʱ�˽����ͬԲ���Բ�У�ͬ������Ȼ������Ե�Բ�ܽ��������ͼ����A��B��C��D��Ϊ��O�ϵĵ㣬���С�C=��D��
С�������֣�����E�ڡ�O�⣬�����D��ֱ��ABͬ�࣬���С�D >��E�� ����ο�С���ó��Ľ��ۣ�����������⣺
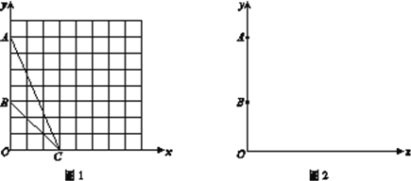
��1����ͼ1����ƽ��ֱ������ϵxOy�У���A������Ϊ(0,7)����B������Ϊ(0,3)����C������Ϊ(3,0) ������ͼ1��������ABC�����Բ��������Ҫ����ͼ�ۼ�����д��������
������![]() �������������һ��D���ҡ�ACB =��ADB�����D������Ϊ________��
�������������һ��D���ҡ�ACB =��ADB�����D������Ϊ________��
(2) ��ͼ2����ƽ��ֱ������ϵxOy�У���A������Ϊ(0,m)����B������Ϊ(0,n)������m>n>0����PΪ![]() ���������ϵ�һ�����㣬����APB�ﵽ���ʱ��ֱ��д����ʱ��P��������
���������ϵ�һ�����㣬����APB�ﵽ���ʱ��ֱ��д����ʱ��P��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����7�֣�ij��ȤС�鿪չ��������ͼ��A��B�������12�ף�С���ӵ�A������AB��������ǰ����2����D����ʱ����CD����ijһ�ƹ��µ�Ӱ��ΪAD��������ԭ������2�뵽���F����ʱ����ͬһ�ƹ��µ�Ӱ��������������������Ӱ��Ϊ1.2�ף�Ȼ�������ٶ���ߵ�ԭ����1.5����������2�뵽���H����ʱ����GH����ͬһ�ƹ��µ�Ӱ��ΪBH����C��E��G��һ��ֱ���ϣ���

��1������ͼ�л�����ԴO���λ�ã���������λ�ڵ�Fʱ������ƹ��µ�Ӱ��FM����д��������
��2����С��ԭ�����ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ж����У��������Ǽ�������ǣ� ��
A.���������εĵ���ȣ�
B.ȫ�������εĶ�Ӧ����ȣ�
C.ֱ��������б���ϵ����ߵ���б�ߵ�һ�룻
D.�߶δ�ֱƽ�����ϵ�����һ�㵽�����߶������˵�ľ�����ȡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����������y=![]() ��k��0������ABCD�Ķ���B��D����A������Ϊ��0����1����AB��x�ᣬCD�����㣨0��2����ABCD�������18�����D�������ǣ�������
��k��0������ABCD�Ķ���B��D����A������Ϊ��0����1����AB��x�ᣬCD�����㣨0��2����ABCD�������18�����D�������ǣ�������

A. ����2��2�� B. ��3��2�� C. ����3��2�� D. ����6��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC��AB=AC��AC�Ĵ�ֱƽ������AB����ֱ���ཻ���õ����Ϊ40������C=______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=��x2+bx+c��һֱ���ཻ��A����1��0����C��2��3�����㣬��y�ύ�ڵ�N���䶥��ΪD��
��1����������ֱ��AC�ĺ�����ϵʽ��
��2����P����������λ��ֱ��AC�Ϸ���һ�����㣬���APC����������ֵ����ʱ��P�����ꣻ
��3�����M��3��n������ʹMN+MDȡ��Сֵʱn��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߳�Ϊ1��С������ƴ��һ��һ���ſ���A1��A2��A3�������ǵ�2��3��4����С���������½ǵĶ��㣬P�ǵ�һ��С���������ϽǵĶ��㣮����PA1A2����PA1A3����PA1A4������Ϊ�ٺ������Ρ��ں������Ρ��ۺ�������������֪��Щ����������һ����������ٺ����������ƣ�����������εĺ���Ϊ��������

A. �� B. �� C. �� D. ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com