
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)连接DE,交AF与O点,试探究线段EG、GF、AF之间的数量关系,并说明理由。

【答案】(1)详见解析;(2)EG2=![]() GFAF,理由详见解析.
GFAF,理由详见解析.
【解析】
(1)依据翻折的性质和平行线的性质证明∠DGF=∠DFG,从而得到GD=DF,根据翻折的性质可证明DG=GE=DF=EF,即可证明四边形EFDG是菱形;(2)连接DE,交AF于点O.由菱形的性质可知GF⊥DE,OG=OF=![]() GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系.
GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系.
(1)∵GE∥DF,
∴∠EGF=∠DFG.
∵由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG.
∴GD=DF.
∴DG=GE=DF=EF.
∴四边形EFDG为菱形.
(2)EG2=![]() GFAF.
GFAF.
证明:如图,连接DE,交AF于点O.

∵四边形EFDG为菱形,
∴GF⊥DE,OG=OF=![]() GF.
GF.
∵∠DOF=∠ADF=90°,∠OFD=∠DFA,
∴△DOF∽△ADF.
∴![]() ,即DF2=FOAF.
,即DF2=FOAF.
∵FO=![]() GF,DF=EG,
GF,DF=EG,
∴EG2=![]() GFAF.
GFAF.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】在“扶贫攻坚”活动中,城南中学计划选购甲、乙两种物品慰问贫困户.已知甲物品的单价比乙物品的单价高10元,若用500元单独购买甲物品与450元单独购买乙物品的数量相同.
(1)请问甲、乙两种物品的单价各为多少?
(2)如果该单位计划购买甲、乙两种物品共55件,总费用不少于5000元且不超过5020元,通过计算得出共有几种选购方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约元旦登山,甲、乙两人距地面的高度y(m)与登山时间x(min)之间的函数图像如图所示,根据图像所提供的信息解答下列问题:
(1)t= min.
(2)若乙提速后,乙登山的上升速度是甲登山的上升速度3倍,
①则甲登山的的上升速度是 m/min;
②请求出甲登山过程中,距地面的高度y(m)与登山时间x(min)之间的函数关系式.
③当甲、乙两人距地面高度差为70m时,求x的值(直接写出满足条件的x值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1).如图①,已知AB∥CD,求证:∠A+∠C=∠E
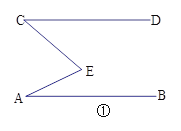
(2)直接写出当点E的位置分别如图②、图③、图④的情形时∠A、∠C、∠AEC之间的关系.
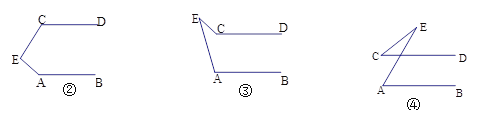
②中∠C、∠A、∠AEC之间的关系为 ;
③中∠C、∠A、∠AEC之间的关系为 ;
④中∠C、∠A、∠AEC之间的关系为 ;
(3)在(2)中的3中情形中任选一种进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.

(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图所示,给出下列说法:
的图象如图所示,给出下列说法:
①![]() ;②方程
;②方程![]() 的根为
的根为![]() ,
,![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 随
随![]() 值的增大而增大;⑤当
值的增大而增大;⑤当![]() 时,
时,![]() .
.
其中正确的个数是

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图:在△ABC中,∠B=90°,∠A=30°,BC=5cm,等腰Rt△DEF中,∠FDE=![]() ,DE=3cm。动点D、E始终在边AB上,当点D从A点沿AC方向移动。
,DE=3cm。动点D、E始终在边AB上,当点D从A点沿AC方向移动。
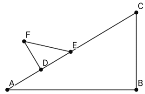
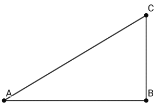
(1)在Rt△DEF沿AC方向移动的过程中,F,C两点之间的距离逐渐_______。(填“不变“变大”或“变小”)
(2)当F、C连线与AB平行时,求AD的长。
(3)以线段AD、FC、BC的长度为三边长的三角形是直角三角形时,求AD的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com