
【题目】AD与BE是△ABC的角平分线,D,E分别在BC,AC上,若AD=AB,BE=BC,则∠C=( )

A. 69° B. ![]() C.
C. ![]() D. 不能确定
D. 不能确定
【答案】C
【解析】分析:根据AD=AB和三角形内角和、外角性质,寻找∠C和∠BAC的关系的表达式;再根据BE=BC,寻找∠C和∠BAC关系的另一种表达式,由此可得关于∠BAC的方程,求得的度数,代入即可求得∠C.
详解:
∵AD=AB,
∴∠ADB=![]() (180°﹣
(180°﹣![]() ∠BAC)=90°﹣
∠BAC)=90°﹣![]() ∠BAC,
∠BAC,
∴∠C=∠ADB﹣∠DAC=![]() (180°﹣
(180°﹣![]() ∠BAC)=90°﹣
∠BAC)=90°﹣![]() ∠BAC﹣
∠BAC﹣![]() ∠BAC=90°﹣
∠BAC=90°﹣![]() ∠BAC;
∠BAC;
∵BE=BC,
∴∠C=∠BEC=∠BAC+∠ABE=∠BAC+![]() (180°﹣
(180°﹣![]() ∠BAC)=∠BAC+45°﹣
∠BAC)=∠BAC+45°﹣![]() ∠BAC=45°+
∠BAC=45°+![]() ∠BAC,
∠BAC,
∴90°﹣![]() ∠BAC=45°+
∠BAC=45°+![]() ∠BAC,
∠BAC,
解得∠BAC=![]() ,
,
∴∠C=90°﹣![]() .
.
故选C.


科目:初中数学 来源: 题型:
【题目】填空,如图所示.

(1)∵![]() (已知),∴_________
(已知),∴_________![]() _________ (______).
_________ (______).
(2)∵![]() (已知),∴_________
(已知),∴_________![]() _________(______).
_________(______).
(3)∵![]() _________
_________![]() (已知),∴
(已知),∴![]() (______).
(______).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个长为8分米,宽为5分米,高为7分米的长方体上,截去一个长为6分米,宽为5分米,深为2分米的长方体后,得到一个如图所示的几何体.一只蚂蚁要从该几何体的顶点A处,沿着几何体的表面到几何体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是 分米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑公司经销甲种型号电脑,每台售价4000元.为了增加收入,电脑公司决定再经销乙种型号电脑.已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台.
(1)有几种进货方案?
(2)如果乙种电脑每台售价为3800元,为打开乙种电脑的销路,公司决定每售出一台乙种电脑,返还顾客现金a元,要使(2)中所有方案获利相同,a值应是多少? 若考虑投入成本最低,则应选择哪种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
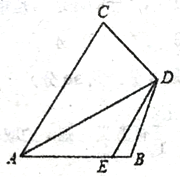
【题目】如图:四边形ABDC中,CD=BD,E为AB上一点,连接DE,且∠CDE=∠B.若∠CAD=∠BAD=30°,AC=5,AB=3,则EB=______________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:

(1)图中自变量是______,因变量是______;
(2)小明家到学校的路程是 米;
(3)小明在书店停留了 分钟;
(4)本次上学途中,小明一共行驶了 米,一共用了 分钟;
(5)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
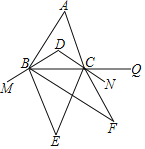
【题目】如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在射线DB、DC、BC上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=( )
A. 30°B. 35°C. 15°D. 25°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的右侧),若数轴上存在一点
的右侧),若数轴上存在一点![]() ,使得
,使得![]() ,则称点
,则称点![]() 为点
为点![]() ,
,![]() 的“
的“![]() 倍分点”,若使得
倍分点”,若使得![]() ,则称点
,则称点![]() 为点
为点![]() ,
,![]() 的“
的“![]() 倍分点”,
倍分点”,![]() ,若使得
,若使得![]() ,则称点
,则称点![]() 为点
为点![]() ,
,![]() 的“
的“![]() 倍分点(
倍分点(![]() 为正整数).请根据上述规定回答下列问题:
为正整数).请根据上述规定回答下列问题:
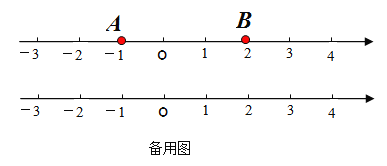
(1)如图,若点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() .
.
①当点![]() 表示数
表示数![]() 时,则
时,则![]() _______;
_______;
②当点![]() 为点
为点![]() ,
,![]() 的“
的“![]() 倍分点”时,求点
倍分点”时,求点![]() 表示的数;
表示的数;
(2)若点![]() 表示数
表示数![]() ,
,![]() ,当点
,当点![]() 为
为![]() 的“
的“![]() 倍分点”时,请直接写出点
倍分点”时,请直接写出点![]() 表示的数.(用含
表示的数.(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com