
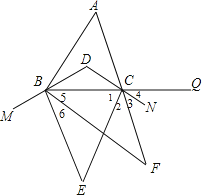
【题目】如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在射线DB、DC、BC上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=( )
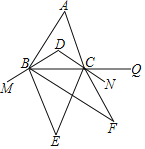
A. 30°B. 35°C. 15°D. 25°
【答案】C
【解析】
先由BD、CD分别平分∠ABC、∠ACB得到∠DBC=![]() ∠ABC,∠DCB=
∠ABC,∠DCB=![]() ∠ACB,在△ABC中根据三角形内角和定理得∠DBC+∠DCB=
∠ACB,在△ABC中根据三角形内角和定理得∠DBC+∠DCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°-∠A)=60°,则根据平角定理得到∠MBC+∠NCB=300°;再由BE、CE分别平分∠MBC、∠BCN得∠5+∠6=
(180°-∠A)=60°,则根据平角定理得到∠MBC+∠NCB=300°;再由BE、CE分别平分∠MBC、∠BCN得∠5+∠6=![]() ∠MBC,∠1=
∠MBC,∠1=![]() ∠NCB,两式相加得到∠5+∠6+∠1=
∠NCB,两式相加得到∠5+∠6+∠1=![]() (∠NCB+∠NCB)=150°,在△BCE中,根据三角形内角和定理可计算出∠E=30°;再由BF、CF分别平分∠EBC、∠ECQ得到∠5=∠6,∠2=∠3+∠4,根据三角形外角性质得到∠3+∠4=∠5+∠F,∠2+∠3+∠4=∠5+∠6+∠E,利用等量代换得到∠2=∠5+∠F,2∠2=2∠5+∠E,再进行等量代换可得到∠F=
(∠NCB+∠NCB)=150°,在△BCE中,根据三角形内角和定理可计算出∠E=30°;再由BF、CF分别平分∠EBC、∠ECQ得到∠5=∠6,∠2=∠3+∠4,根据三角形外角性质得到∠3+∠4=∠5+∠F,∠2+∠3+∠4=∠5+∠6+∠E,利用等量代换得到∠2=∠5+∠F,2∠2=2∠5+∠E,再进行等量代换可得到∠F=![]() ∠E.
∠E.
解:∵BD、CD分别平分∠ABC、∠ACB,∠A=60°,
∴∠DBC=![]() ∠ABC,∠DCB=
∠ABC,∠DCB=![]() ∠ACB,
∠ACB,
∴∠DBC+∠DCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°﹣∠A
(180°﹣∠A![]() ×(180°﹣60°)=60°,
×(180°﹣60°)=60°,
∴∠MBC+∠NCB=360°﹣60°=300°,
∵BE、CE分别平分∠MBC、∠BCN,
∴∠5+∠6=![]() ∠MBC,∠1=
∠MBC,∠1=![]() ∠NCB,
∠NCB,
∴∠5+∠6+∠1=![]() (∠NCB+∠NCB)=150°,
(∠NCB+∠NCB)=150°,
∴∠E=180°﹣(∠5+∠6+∠1)=180°﹣150°=30°,
∵BF、CF分别平分∠EBC、∠ECQ,
∴∠5=∠6,∠2=∠3+∠4,
∵∠3+∠4=∠5+∠F,∠2+∠3+∠4=∠5+∠6+∠E,
即∠2=∠5+∠F,2∠2=2∠5+∠E,
∴2∠F=∠E,
∴∠F=![]() ∠E=
∠E=![]() ×30°=15°.
×30°=15°.
故选:C.


科目:初中数学 来源: 题型:
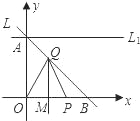
【题目】如图所示,已知直线L过点A(0,1)和B(1,0),P是x轴正半轴上的动点,OP的垂直平分线交L于点Q,交x轴于点M.
(1)直接写出直线L的解析式;
(2)设OP=t,△OPQ的面积为S,求S关于t的函数关系式;并求出当0<t<2时,S的最大值;
(3)直线L1过点A且与x轴平行,问在L1上是否存在点C,使得△CPQ是以Q为直角顶点的等腰直角三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
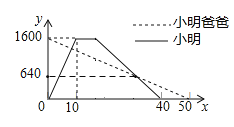
【题目】小明从家出发到公园晨练,在公园锻炼一段时间后按原路返回,同时小明爸爸从公园按小明的路线返回家中.如图是两人离家的距离![]() (米)与小明出发的时间
(米)与小明出发的时间![]() (分)之间的关系,则小明出发______分钟后与爸爸相遇.
(分)之间的关系,则小明出发______分钟后与爸爸相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(﹣4,4),一个以A为顶点的45°角绕点A旋转,角的两边分别交x轴正半轴,y轴负半轴于E、F,连接EF.当△AEF是直角三角形时,点E的坐标是_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小李某天下午运营全是在东西走向的人民大道上进行的,如果规定向东为正,向西为负,他这天下午行驶里程如下:(单位:千米)
+15, -3, +14,-11,+10,-12,+4,-15,+16,-18
(1)他将最后一名乘客送到目的地时,距下午出车地点是多少千米?
(2)若汽车耗油量为![]() 升∕千米,这天下午共耗油多少升
升∕千米,这天下午共耗油多少升
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的![]() ?若存在求出此时点M的坐标;若不存在,说明理由.
?若存在求出此时点M的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平面直角坐标系中两定点A(﹣1,0)、B(4,0),抛物线y=ax2+bx﹣2(a≠0)过点A,B,顶点为C,点P(m,n)(n<0)为抛物线上一点.
(1)求抛物线的解析式和顶点C的坐标;
(2)当∠APB为钝角时,求m的取值范围;
(3)若m>![]() ,当∠APB为直角时,将该抛物线向左或向右平移t(0<t<
,当∠APB为直角时,将该抛物线向左或向右平移t(0<t<![]() )个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首位依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.
)个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首位依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com