
����Ŀ����ͼ��������y=-x2+mx+n��x�ύ��A,B���㣬y���ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪A(-1,0),C(0,3)
�������ߵĽ���ʽ��
�������ߵĶԳ������Ƿ����P�㣬ʹ�SPCD����CDΪ���ĵ��������Σ�������ڣ�ֱ��д����P�����꣬��������ڣ���˵�����ɣ�
��E���߶�BC�ϵ�һ�����㣬����E��x��Ĵ������������ཻ�ڵ�F��
����ֱ��BC �Ľ���ʽ
�ڵ���E�˶���ʲôλ��ʱ���ı���CDBF�����������ı���CDBF������������ʱ��E������

���𰸡���1��y=��![]() x2+
x2+![]() x+2����2��P1��
x+2����2��P1��![]() ��4����P2��
��4����P2��![]() ��
�� ![]() ����P3��
����P3��![]() ����
����![]() ������3����y=��
������3����y=��![]() x+2����S�ı���CDBF��������=
x+2����S�ı���CDBF��������=![]() ��E��2��1��
��E��2��1��
�������������������1���ɴ���ϵ����������Ԫһ�η��������m��n��ֵ���ɣ�
��2����ͼ1�У��������������ۢٵ�PD=DCʱ����CP=CDʱ���ֱ�д����P���꼴�ɣ�
��3�������BC�Ľ���ʽ�������E�ĺ�����Ϊa�����ı���CDBF�����=S��BCD+S��CEF+S��BEF���S��a�Ĺ�ϵʽ���ɶ��κ��������ʾͿ���������ۣ�
�����������1����������y=-![]() x2+mx+n����A��-1��0����C��0��2����
x2+mx+n����A��-1��0����C��0��2����
��ã� 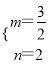 ��
��
�������ߵĽ���ʽΪ��y=-![]() x2+
x2+![]() x+2��
x+2��
��2����ͼ1��

��y=-![]() x2+
x2+![]() x+2��
x+2��
��y=-![]() ��x-
��x-![]() ��2+
��2+![]() ��
��
�������ߵĶԳ�����ֱ��x=![]() ��
��
��OD=![]() ��
��
��C��0��3����
��OC=23
��Rt��OCD�У��ɹ��ɶ�������CD=![]() ��
��
�ߡ�CDP����CDΪ���ĵ��������Σ�
��CP1=DP2=DP3��
��CH��x����H��
��HP1=HD=2��
��DP1=4��
��P1��![]() ��4����P2��
��4����P2��![]() ��
�� ![]() ����P3��
����P3��![]() ��-
��-![]() ����
����
��3����y=0ʱ��0=-![]() x2+
x2+![]() x+2
x+2
��x1=-1��x2=4��
��B��4��0����
��ֱ��BC�Ľ���ʽΪy=kx+b����ͼ��![]() ��
��
��ã� 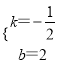 ��
��
��ֱ��BC�Ľ���ʽΪ��y=-![]() x+2��
x+2��
��ͼ2��

����C��CM��EF��M����E��a��-![]() a+2����F��a��-
a+2����F��a��-![]() a2+
a2+![]() a+2����
a+2����
��EF=-![]() a2+
a2+![]() a+2-��-
a+2-��-![]() a+2��=-
a+2��=-![]() a2+2a��0��x��4����
a2+2a��0��x��4����
��S�ı���CDBF=S��BCD+S��CEF+S��BEF=![]() BDOC+
BDOC+![]() EFCM+
EFCM+![]() EFBN��
EFBN��
=![]() ��
��![]() ��2+
��2+![]() a��-
a��-![]() a2+2a��+
a2+2a��+![]() ��4-a����-
��4-a����-![]() a2+2a����
a2+2a����
=-a2+4a+![]() ��0��x��4����
��0��x��4����
=-��a-2��2+![]()
��a=2ʱ��S�ı���CDBF��������=![]() ��
��
��E��2��1����


 ������ȫ�̼����ĩ���100��ϵ�д�
������ȫ�̼����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ��(x��y)(x��2y)��(3x��2y)(x+3y)������x��4��y����1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��O����AB���ڰ뾶������OB���ӳ�ʹBC=OB��
��1����ABC=�� ����
��2��AC���O��ʲô��ϵ����֤����Ľ��ۣ�
��3���ڡ�O�ϣ��Ƿ���ڵ�D��ʹ��AD=AC�������ڣ��뻭��ͼ�Σ�������֤�����������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
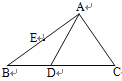
����Ŀ����ͼ����ABC�У�DΪBC���ϵĵ㣬��CAD����CDA��EΪAB�ߵ��е㣮
��1���߹���ͼ������C��ƽ����CF����AD�ڵ�F��������ͼ�ۼ�����д��������
��2������EF��EF��BC��ʲôλ�ù�ϵ��Ϊʲô��
��3�����ı���BDFE�����Ϊ9�����ABD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬʱ��ʼ��ժӣ�ң���ƽ��ÿСʱ��ժ8����ӣ�ң���ƽ��ÿСʱ��ժ7����ӣ�ҡ���ժͬʱ�����״�����ժ��ӣ����ȡ��1��������ң���ʱ���˵�ӣ��һ���ࡣ���Dz�ժӣ�����˶ʱ��?�����Dz�ժ��xСʱ�����������з�������ȷ���ǣ� ��
A.8x-1=7x+1
B.8x-1=7x
C.8x+l=7x
D.8x+l=7x-1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ݰ���˹̹������ۣ��������Ͼ���1����ʱ������ɴ���ֻ����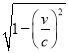 ��.��ʽ�ڵ�v��ָ����ɴ����ٶȣ�c��ָ���٣�Լ 30��ǧ��/�룩���ٶ���һ�����ֵܣ����23�꣬�ܵ� 20�꣬�������Թ���0. 98�����ٶȷ��е�����ɴ�������5���������к������.���5����ָ�����ϵ�5�꣬���Եܵܵ�����Ϊ25��,���Ǹ������������ʱ����ֻ����һ�ֻ꣬��24�꣬���������������к�ܱܵȸ�練������1�꣬���������Ϲ�ʽ��֤һ���������.
��.��ʽ�ڵ�v��ָ����ɴ����ٶȣ�c��ָ���٣�Լ 30��ǧ��/�룩���ٶ���һ�����ֵܣ����23�꣬�ܵ� 20�꣬�������Թ���0. 98�����ٶȷ��е�����ɴ�������5���������к������.���5����ָ�����ϵ�5�꣬���Եܵܵ�����Ϊ25��,���Ǹ������������ʱ����ֻ����һ�ֻ꣬��24�꣬���������������к�ܱܵȸ�練������1�꣬���������Ϲ�ʽ��֤һ���������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ͬһ�ۿ�ͬʱ����������У��״�˳ˮ���Ҵ���ˮ�������ھ�ˮ�е��ٶȶ���50ǧ��/ʱ��ˮ���ٶ���aǧ��/ʱ��2Сʱ��״����Ҵ��ຽ��_____ǧ�ף�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com