
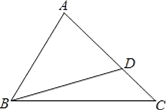
【题目】如图,已知⊙O的弦AB等于半径,连接OB并延长使BC=OB.
(1)∠ABC= .
(2)AC与⊙O有什么关系?请证明你的结论;
(3)在⊙O上,是否存在点D,使得AD=AC?若存在,请画出图形,并给出证明;若不存在,请说明理由.

【答案】(1)120°;(2)AC是⊙O的切线,证明见解析;(3)存在.证明见解析.
【解析】解:(1)120°;……………………………………………………………1分
(2)AC是⊙O的切线.……………………………………………………3分
证法一
∵AB=OB=OA,∴△OAB为等边三角形,…………………………4分
∴∠OBA=∠AOB=60°.……………………………………………5分
∵BC=BO,∴BC=BA,
∴∠C=∠CAB,……………………………………………………………6分
又∵∠OBA=∠C+∠CAB=2∠C,
即2∠C=60°,∴∠C=30°,………………………………………7分
在△OAC中,∵∠O+∠C=60°+30°=90°,
∴∠OAC=90°,…………………………………………………………8分
∴AC是⊙O的切线;
证法二:
∵BC=OB,∴点B为边OC的中点,……………………………………4分
即AB为△OAC的中位线,…………………………………………………5分
∵AB=OB=BC,即AB是边OC的一半,……………………………6分
∴△OAC是以OC为斜边的直角三角形,…………………………………7分
∴∠OAC=90°,…………………………………………………………8分
∴AC是⊙O的切线;
(3)存在.……………………………………………………………………9分
方法一:
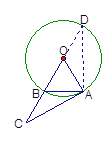
如图2,延长BO交⊙O于点D,即为所求的点.…………………………10分
证明如下:
连结AD,∵BD为直径,∴∠DAB=90°.…………………………11分
在△CAO和△DAB中,
∵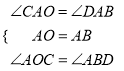 ,∴△CAO≌△DAB(ASA),………………12分
,∴△CAO≌△DAB(ASA),………………12分
∴AC=AD.…………………………………………………………………13分
(也可由OC=BD,根据AAS证明;或HL证得,或证△ABC≌△AOD)
方法二:
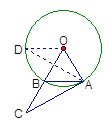
如图3,画∠AOD=120°,……………………………………………10分
OD交⊙O于点D,即为所求的点.…………………………………………11分
∵∠OBA=60°,
∴∠ABC=180°-60°=120°.
在△AOD和△ABC中,
∵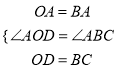 ,∴△AOD≌△ABC(SAS),………………12分
,∴△AOD≌△ABC(SAS),………………12分
∴AD=AC.…………………………………………………………………13分
(1)由已知可知△AOB为等边三角形,利用平角求出∠ABC的度数
(2)利用直角三角形的性质求出∠OAC=90°,从而得出结论
(3)延长BO交⊙O于点D,即为所求的点,利用全等三角形求证


科目:初中数学 来源: 题型:
【题目】如图:△ABC中,∠C=45°,点D在AC上,且∠ADB=60°,AB为△BCD外接圆的切线.
(1)用尺规作出△BCD的外接圆(保留作图痕迹,可不写作法);
(2)求∠A的度数;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一间中学就读的李浩与王真是两邻居,平时他们一起骑自行车上学,清明节后的一天,李浩因有事,比王真迟了10分钟出发,为了能赶上王真,李浩用了王真速度的1.2倍骑车追赶,结果他们在学校大门处相遇,已知他们家离学校大门处的骑车距离为15千米.求王真的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个纸盒里装有四张除数字以外完全相同卡片,四张卡片上的数字分别为1,2,3,4.先从纸盒里随机取出一张,记下数字为![]() ,再从剩下的三张中随机取出一张,记下数字为
,再从剩下的三张中随机取出一张,记下数字为![]() ,这样确定了点P的坐标(
,这样确定了点P的坐标(![]() ,
, ![]() ).
).
(1)请你运用画树状图或列表的方法,写出点P所有可能的坐标;
(2)求点P(![]() ,
, ![]() )在函数
)在函数![]() =-
=-![]() +4图象上的概率.
+4图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+mx+n与x轴交于A,B两点,y与轴交于点C,抛物线的对称轴交x轴于点D。已知A(-1,0),C(0,3)
求抛物线的解析式;
在抛物线的对称轴上是否存在P点,使⊿PCD是以CD为腰的等腰三角形,如果存在,直接写出点P的坐标,如果不存在,请说明理由;
点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,
①求直线BC 的解析式
②当点E运动到什么位置时,四边形CDBF的面积最大?求四边形CDBF的最大面积及此时点E的坐标

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com