
分析 根据平方差公式,可分母有理化.
解答 解:都正确,
甲:原式=$\frac{(a-b)(\sqrt{a}-\sqrt{b})}{(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})}$=$\frac{(a-b)(\sqrt{a}-\sqrt{b})}{a-b}$=$\sqrt{a}$-$\sqrt{b}$,甲分子分母都乘以相同的二次根式;
原式=$\frac{(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})}{\sqrt{a}+\sqrt{b}}$=$\sqrt{a}$-$\sqrt{b}$,乙对分子进行平方差公式分解因式.
点评 本题考查了分母有理化,利用平方差公式是解题关键.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
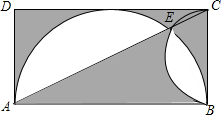 如图,长方形的长AB为8厘米,宽BC为4厘米,分别以AB、BC为直径画半圆,两个半圆的交点E在线段AC上,求阴影部分的面积.(π取3.14)
如图,长方形的长AB为8厘米,宽BC为4厘米,分别以AB、BC为直径画半圆,两个半圆的交点E在线段AC上,求阴影部分的面积.(π取3.14)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
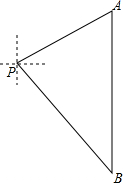 如图,一艘轮船位于灯塔P的北偏东65°方向8海里远的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东39°方向上的B处.B距离P有多远?(精确到0.1海里)
如图,一艘轮船位于灯塔P的北偏东65°方向8海里远的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东39°方向上的B处.B距离P有多远?(精确到0.1海里)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
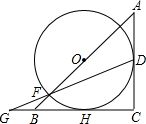 如图,在等腰直角三角形ABC中,以斜边AB的中点O为圆心的⊙O与AC相切于点D,与AB相交于点E,F,DF与CB的延长线交于点G.
如图,在等腰直角三角形ABC中,以斜边AB的中点O为圆心的⊙O与AC相切于点D,与AB相交于点E,F,DF与CB的延长线交于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com