
【题目】(8分)已知购买1个足球和1个篮球共需130元,购买2个足球和1个篮球共需180元.
(1)求每个足球和每个篮球的售价;
(2)如果某校计划购买这两种球共54个,总费用不超过4000元,问最多可买多少个篮球?
科目:初中数学 来源: 题型:
【题目】如图,小明的数学作业本上都是等距的横线,相邻两条横线的距离都是1厘米,他把一个等腰直角三角板放ABC(∠ACB=90°,AC=BC)在本子上,点A、B、C恰好都在横线上,则斜边AB的长度为( )

A.10B.3![]() C.4
C.4![]() D.6
D.6![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,A、B、C三点的坐标分别为(﹣2,4)、(﹣3,0)、(4,1).
(1)画出△ABC;
(2)△ABC的面积为 ;
(3)△ABC向上平移3个单位长度,向左平移1个单位长度.请画出图形并写出对应点A1B1C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】又到了一年中的春游季节.某班学生利用周末去参观“三军会师纪念塔”.下面是两位同学的一段对话:
甲:我站在此处看塔顶仰角为60°;
乙:我站在此处看塔顶仰角为30°;
甲:我们的身高都是1.6m;
乙:我们相距36m.
请你根据两位同学的对话,计算纪念塔的高度.(精确到1米)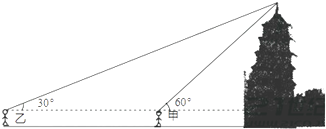
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一圆锥形粮堆,其侧面展开图是半径为6m的半圆,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程长为( )
A.3m
B.![]() m
m
C.![]() m
m
D.4m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条高铁线A,B,C三个车站的位置如图所示.已知B,C两站之间相距530千米.高铁列车从B站出发,向C站方向匀速行驶,经过13分钟距A站165千米;经过80分钟距A站500千米.
![]()
(1)求高铁列车的速度和AB两站之间的距离.(2)如果高铁列车从A站出发,开出多久可以到达C站?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小数在数学外小组活动中遇到这样一个问题:如果α、β都为锐角,且tanα= ![]() ,tanβ=
,tanβ= ![]() .求α+β的度数.
.求α+β的度数.
(1)小敏是这样解决问题的:如图1,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,且BA,BC在直线BD的两侧,连接AC,可证得△ABC是等腰直角三角形,因此可求得α+β=∠ABC=°.
(2)请你参考小敏思考问题的方法解决问题:如果α,β都为锐角,当tanα=4,tanβ= ![]() 时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=α﹣β,由此可得α﹣β=°.
时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=α﹣β,由此可得α﹣β=°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了一可以自由转动的转盘,AB为转盘直径,如图所示,并规定:顾客消费100元(含100元)以上,就能获得一次转盘的机会,如果转盘停止后,指针正好对准9折、8折、7折区域,顾客就可以获得相应的优惠.
(1)某顾客正好消费99元,是否可以获得相应的优惠.
(2)某顾客正好消费120元,他转一次转盘获得三种打折优惠的概率分别是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com