
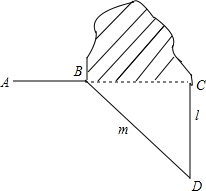
 小明爸爸给小明出了一道题:如图,修公路AB遇到一座山,于是要修一条隧道BC.已知A,B,C在同一条直线上,为了在小山的两侧B,C同时施工.过点B作一直线m(在山的旁边经过),过点C作一直线l与m相交于D点,经测量∠ABD=130°,∠D=40°,BD=1000米,CD=800米.若施工队每天挖100米,求施工队几天能挖完?
小明爸爸给小明出了一道题:如图,修公路AB遇到一座山,于是要修一条隧道BC.已知A,B,C在同一条直线上,为了在小山的两侧B,C同时施工.过点B作一直线m(在山的旁边经过),过点C作一直线l与m相交于D点,经测量∠ABD=130°,∠D=40°,BD=1000米,CD=800米.若施工队每天挖100米,求施工队几天能挖完? 科目:初中数学 来源: 题型:填空题
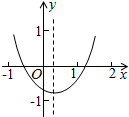 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0,其中所有正确结论的序号是①④.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0,其中所有正确结论的序号是①④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com