
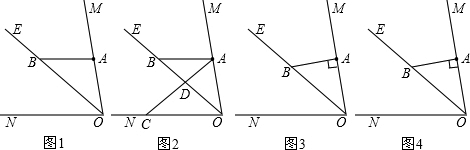
分析 (1)①利用角平分线的性质求出∠ABO的度数;
②利用角平分线的性质和平行线的性质求得∠OAC=60°;
(2)需要分类讨论:当点D在线段OB上和点D在射线BE上两种情况.
解答 解:(1)①∵∠MON=80°,OE平分∠MON.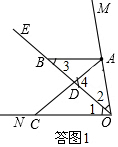
∴∠AOB=∠BON=40°,
∵AB∥ON,
∴∠ABO=40°
故答案是:40°;
②如答图1,∵∠MON=80°,且OE平分∠MON,
∴∠1=∠2=40°,
又∵AB∥ON,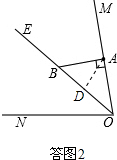
∴∠3=∠1=40°,
∵∠BAD=∠ABD,
∴∠BAD=40°
∴∠4=80°,
∴∠OAC=60°,即x=60°.
(2)存在这样的x,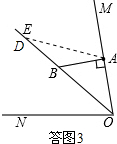
①如答图2,当点D在线段OB上时,
若∠BAD=∠ABD,则x=40°;
若∠BAD=∠BDA,则x=25°;
若∠ADB=∠ABD,则x=10°.
②如答图3,当点D在射线BE上时,因为∠ABE=130°,且三角形的内角和为180°,
所以只有∠BAD=∠BDA,此时x=65°,C不在ON上,舍去;
综上可知,存在这样的x的值,使得△ADB中有两个相等的角,
且x=10°、25°、40°.
点评 本题考查的是平行线的性质,三角形的内角和定理和三角形的外角性质的应用,注意:三角形的内角和等于180°,三角形的一个外角等于和它不相邻的两个内角之和.


科目:初中数学 来源: 题型:解答题
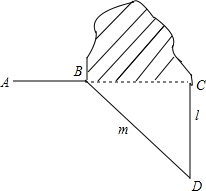 小明爸爸给小明出了一道题:如图,修公路AB遇到一座山,于是要修一条隧道BC.已知A,B,C在同一条直线上,为了在小山的两侧B,C同时施工.过点B作一直线m(在山的旁边经过),过点C作一直线l与m相交于D点,经测量∠ABD=130°,∠D=40°,BD=1000米,CD=800米.若施工队每天挖100米,求施工队几天能挖完?
小明爸爸给小明出了一道题:如图,修公路AB遇到一座山,于是要修一条隧道BC.已知A,B,C在同一条直线上,为了在小山的两侧B,C同时施工.过点B作一直线m(在山的旁边经过),过点C作一直线l与m相交于D点,经测量∠ABD=130°,∠D=40°,BD=1000米,CD=800米.若施工队每天挖100米,求施工队几天能挖完?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
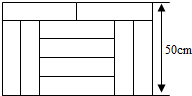 如图,宽为50cm的长方形团由10个形状大小完全相同的小长方形拼成,其汇总一个小长方形的面积为( )
如图,宽为50cm的长方形团由10个形状大小完全相同的小长方形拼成,其汇总一个小长方形的面积为( )| A. | 400cm2 | B. | 500cm2 | C. | 600cm2 | D. | 4000cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
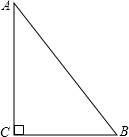 如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,AB=10cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm.设运动的时间为t秒.
如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,AB=10cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm.设运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
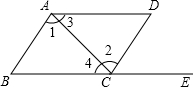 如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( )
如图,点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( )| A. | ∠3=∠4 | B. | ∠B=∠DCE | C. | ∠1=∠2 | D. | ∠D+∠DAB=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,1) | B. | (2,-7) | C. | (6,-3) | D. | (-2,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
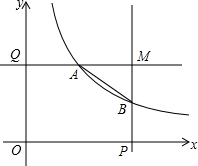 如图,在平面直角坐标系中,P,Q分别是x轴,y轴的正半轴上两动点,OP=2,OQ=k,分别过P,Q作坐标轴的垂线,交反比例函数y=$\frac{k}{x}$于点A,B两垂线交于点M,点E为线段OP上一动点.
如图,在平面直角坐标系中,P,Q分别是x轴,y轴的正半轴上两动点,OP=2,OQ=k,分别过P,Q作坐标轴的垂线,交反比例函数y=$\frac{k}{x}$于点A,B两垂线交于点M,点E为线段OP上一动点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
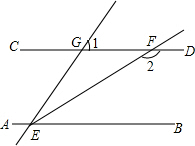 如图,已知直线AB∥CD,∠BEG的平分线EF交CD于点F,若∠1=42°,则∠2等于( )
如图,已知直线AB∥CD,∠BEG的平分线EF交CD于点F,若∠1=42°,则∠2等于( )| A. | 159° | B. | 148° | C. | 142° | D. | 138° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com