
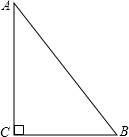
 如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,AB=10cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm.设运动的时间为t秒.
如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,AB=10cm.若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm.设运动的时间为t秒.分析 (1)先求出△ABC的周长为24cm,所以当CP把△ABC的周长分成相等的两部分时,点P在AB上,此时CA+AP=BP+BC=12cm,再根据时间=路程÷速度即可求解;
(2)根据中线的性质可知,点P在AB中点时,CP把△ABC的面积分成相等的两部分,进而求解即可;
(3)分两种情况:①P在AC上;②P在AB上.
解答 解:(1)△ABC中,∵AC=8cm,BC=6cm,AB=10cm,
∴△ABC的周长=8+6+10=24cm,
∴当CP把△ABC的周长分成相等的两部分时,点P在AB上,此时CA+AP=BP+BC=12cm,
∴2t=12,t=6;
(2)当点P在AB中点时,CP把△ABC的面积分成相等的两部分,此时CA+AP=8+5=13(cm),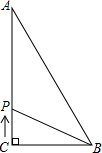 ∴2t=13,t=6.5;
∴2t=13,t=6.5;
(3)分两种情况:
①当P在AC上时,
∵△BCP的面积=12,
∴$\frac{1}{2}$×6×CP=12,
∴CP=4,
∴2t=4,t=2;
②当P在AB上时,
∵△BCP的面积=12=△ABC面积的一半,
∴P为AB中点,
∴2t=13,t=6.5.
故答案为6秒;6.5秒.
点评 本题考查了一元一次方程的应用,三角形的周长与面积,三角形的中线,难度适中.利用分类讨论的思想是解(3)题的关键.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
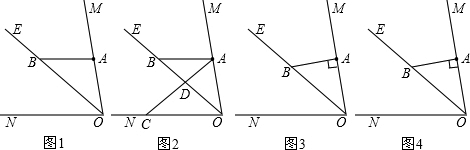
 如图,在?ABCD中,O为对角线AC的中点,EF经过点O并与AB,CD分别相交于点E,F.
如图,在?ABCD中,O为对角线AC的中点,EF经过点O并与AB,CD分别相交于点E,F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
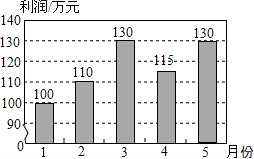 某企业1~5月份的利润情况如图所示,则下列说法中正确的是( )
某企业1~5月份的利润情况如图所示,则下列说法中正确的是( )| A. | 1~2月份利润的增长快于2~3月份利润的增长 | |
| B. | 1~4月份利润的极差于1~5月份利润的极差不同 | |
| C. | 1~5月份利润的中位数是120万元 | |
| D. | 1~5月份利润的众数是130万元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com