
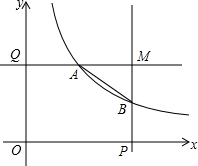
 ��ͼ����ƽ��ֱ������ϵ�У�P��Q�ֱ���x�ᣬy����������������㣬OP=2��OQ=k���ֱ��P��Q��������Ĵ��ߣ�������������y=$\frac{k}{x}$�ڵ�A��B�����߽��ڵ�M����EΪ�߶�OP��һ���㣮
��ͼ����ƽ��ֱ������ϵ�У�P��Q�ֱ���x�ᣬy����������������㣬OP=2��OQ=k���ֱ��P��Q��������Ĵ��ߣ�������������y=$\frac{k}{x}$�ڵ�A��B�����߽��ڵ�M����EΪ�߶�OP��һ���㣮���� ��1������A���߶�QM��ʱ�����A��������Ϊk�����뷴������������ʽ�õ�A�ĺ�����Ϊ1����B�ĺ�����Ϊ2�����뷴���������Ľ���ʽ�õ�B��������Ϊ$\frac{k}{2}$��������õ�M������Ϊ��2��k������AM=2-1=1��BM=k-$\frac{k}{2}$=$\frac{k}{2}$��
��2�����÷������۵�˼�룬����ABEΪֱ�ǣ���BA��BE��BA=BE������EABΪֱ�ǣ���AB��AE��AB=AE������EABΪֱ�ǣ���AB��AE��AB=AE����������֮����빫ʽ����ֱ�ߴ�ֱ��ʱ��б�ʵĹ�ϵ���ô���˼��ɽ�ý����
��� �⣺��1����OP=2��OQ=k��
���Q������0��k������P��������2��0����
�ߵ�A���߶�QM�ϣ�
���A��������Ϊk��
���뷴������������ʽ�ã�k=$\frac{k}{x}$����ã�x=1��
�ߵ�B��ֱ��MP�ϣ�
���B�ĺ�����Ϊ2��
���뷴���������Ľ���ʽ�ã�y=$\frac{k}{2}$��
������õ�M������Ϊ��2��k����
��AM=2-1=1��
BM=k-$\frac{k}{2}$=$\frac{k}{2}$��
��2����E��x0��0����0��x0��2����
����ABEΪֱ�ǣ���BA��BE��BA=BE��
��BA=BE��
��1+${��k-\frac{k}{2}��}^{2}$=${{��x}_{0}-2��}^{2}$+${��\frac{k}{2}��}^{2}$��
��ã�x0=1��x0=3����ȥ����
��x0=1��
��E��1��0����
��BA2+BE2=AE2��BA=BE��
��2BA2=AE2��
��2��$\frac{{k}^{2}}{4}$+1��=k2����ã�k=2��k=-2����ȥ����
����AEBΪֱ�ǣ���EA��EB��EA=EB��
��$\left\{\begin{array}{l}{��1{-x}_{0}����2{-x}_{0}��{+��\frac{k}{2}��}^{2}=0}\\{{��1{-x}_{0}��}^{2}{+k}^{2}{=��2{-x}_{0}��}^{2}{+��\frac{k}{4}��}^{2}}\end{array}\right.$��
��ã�x0=3����ȥ����${x}_{0}=\frac{4}{3}$��k=$\frac{2}{3}$��
��${x}_{0}=\frac{4}{3}$ʱ��k=$\frac{2}{3}$��
����EABΪֱ�ǣ���AB��AE��AB=AE��
��$\left\{\begin{array}{l}{{x}_{0}-1+\frac{{k}^{2}}{2}=0}\\{1+\frac{{k}^{2}}{4}{={��x}_{0}-1��}^{2}{+k}^{2}}\end{array}\right.$��
��ã�${x}_{0}=\frac{1}{2}$��x0=3����ȥ����
��${x}_{0}=\frac{1}{2}$ʱ��k=1��
�൱k=2��k=$\frac{2}{3}$��k=1ʱ����ABE�ǵ���ֱ�������Σ�
���� ������Ҫ�����˷�����������ͼ������ʡ������뺯��ͼ��Ĺ�ϵ�ȣ��������ۣ���ϵ���ֱ�������ε����ʣ�����ͼ�������⣬��ͼ�ϻ�ȡ���õ���Ϣ���ǽ�������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
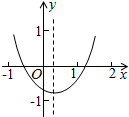 ��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ���������½��ۣ���a+b+c��0����a-b+c��0����b+2a��0����abc��0������������ȷ���۵�����Ǣ٢ܣ�
��֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ���������½��ۣ���a+b+c��0����a-b+c��0����b+2a��0����abc��0������������ȷ���۵�����Ǣ٢ܣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 12 | B�� | 14 | C�� | 12��14 | D�� | ���϶����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����?ABCD�У�OΪ�Խ���AC���е㣬EF������O����AB��CD�ֱ��ཻ�ڵ�E��F��
��ͼ����?ABCD�У�OΪ�Խ���AC���е㣬EF������O����AB��CD�ֱ��ཻ�ڵ�E��F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
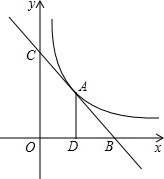 ��ֱ֪��y=k1x+b��˫����$y=\frac{k_2}{x}$�ཻ�ڵ�A��2��4��������x�ᡢy��ֱ���B��C���㣬AD��ֱƽ��OB������ΪD����ֱ�ߺ�˫���ߵĽ���ʽ��
��ֱ֪��y=k1x+b��˫����$y=\frac{k_2}{x}$�ཻ�ڵ�A��2��4��������x�ᡢy��ֱ���B��C���㣬AD��ֱƽ��OB������ΪD����ֱ�ߺ�˫���ߵĽ���ʽ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB�ǡ�O�����ߣ�BΪ�е㣬Բ��O��AC�ϣ���A=30�㣬DΪ$\widehat{BC}$���е㣮
��ͼ��AB�ǡ�O�����ߣ�BΪ�е㣬Բ��O��AC�ϣ���A=30�㣬DΪ$\widehat{BC}$���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com