
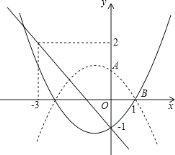
【题目】在平面直角坐标系![]() 中,二次函数
中,二次函数![]() 的图象与
的图象与![]() 轴正半轴交于
轴正半轴交于![]() 点.
点.

![]() 求证:该二次函数的图象与
求证:该二次函数的图象与![]() 轴必有两个交点;
轴必有两个交点;
![]() 设该二次函数的图象与
设该二次函数的图象与![]() 轴的两个交点中右侧的交点为点
轴的两个交点中右侧的交点为点![]() ,若
,若![]() ,将直线
,将直线![]() 向下平移
向下平移![]() 个单位得到直线
个单位得到直线![]() ,求直线
,求直线![]() 的解析式;
的解析式;
![]() 在
在![]() 的条件下,设
的条件下,设![]() 为二次函数图象上的一个动点,当
为二次函数图象上的一个动点,当![]() 时,点
时,点![]() 关于
关于![]() 轴的对称点都在直线
轴的对称点都在直线![]() 的下方,求
的下方,求![]() 的取值范围.
的取值范围.
【答案】![]() 证明见解析;
证明见解析;![]() ;
;![]() .
.
【解析】
(1)直接利用根的判别式,结合完全平方公式求出△的符号进而得出答案;
(2)首先求出B,A点坐标,进而求出直线AB的解析式,再利用平移规律得出答案;
(3)根据当-3<p<0时,点M关于x轴的对称点都在直线l的下方,当p=0时,q=1;当p=-3时,q=12m+4;结合图象可知:-(12m+4)≤2,即可得出m的取值范围.
![]() 令
令![]() ,则
,则
![]() ,
,
∵二次函数图象与![]() 轴正半轴交于
轴正半轴交于![]() 点,
点,
∴![]() ,且
,且![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴该二次函数的图象与轴必有两个交点;
![]() 令
令![]() ,
,
解得:![]() ,
,![]() ,
,
由![]() 得
得![]() ,故
,故![]() 的坐标为
的坐标为![]() ,
,
又因为![]() ,
,
所以![]() ,即
,即![]() ,
,
则可求得直线![]() 的解析式为:
的解析式为:![]() .
.
再向下平移![]() 个单位可得到直线
个单位可得到直线![]() ;
;
![]() 由
由![]() 得二次函数的解析式为:
得二次函数的解析式为:![]() .
.
∵![]() 为二次函数图象上的一个动点,
为二次函数图象上的一个动点,
∴![]() .
.
∴点![]() 关于轴的对称点
关于轴的对称点![]() 的坐标为
的坐标为![]() .
.
∴![]() 点在二次函数
点在二次函数![]() 上.
上.
∵当![]() 时,点
时,点![]() 关于
关于![]() 轴的对称点都在直线
轴的对称点都在直线![]() 的下方,
的下方,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
结合图象可知:![]() ,
,
解得:![]() .
.
∴![]() 的取值范围为:
的取值范围为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,CE和BD交于点O,AO的延长线交BC于点F,则图中全等的三角形有( )

A.8对B.7对C.6对D.5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴的一个交点
轴的一个交点![]() 在点
在点![]() 和
和![]() 之间,其部分图象如图所示,则以下结论:①
之间,其部分图象如图所示,则以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④方程以
;④方程以![]() 有两个的实根,其中正确的个数为( )
有两个的实根,其中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论:①AP⊥BC;②AS=AR;③QP∥AR;④△BRP≌△QSP.正确的有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于![]() 的一元二次方程
的一元二次方程![]() 有两个整数根且乘积为正,关于
有两个整数根且乘积为正,关于![]() 的一元二次方程
的一元二次方程![]() 同样也有两个整数根且乘积为正,给出三个结论:①这两个方程的根都负根;②
同样也有两个整数根且乘积为正,给出三个结论:①这两个方程的根都负根;②![]() ;③
;③![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC 中,∠ACB=90°,AC=80,BC=60, 点D 从点 B 出发,在线段 BA 上以每秒 4 个单位长度的速度向终点A 运动,连结CD. 设点D 运动的时间为 t 秒.
(1)用含 t 的代数式表示 BD 的长.
(2)求AB 的长及 AB 边上的高.
(3)当△BCD 为等腰三角形时,直接写出 t 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级![]() 班有
班有![]() 名同学,其中男生
名同学,其中男生![]() 人.在一节数学课上,老师叫班上每个同学把自己的名字(没有同名)各写在一张大小、形状都相同的小卡片上,并放入一个盒子里摇匀.
人.在一节数学课上,老师叫班上每个同学把自己的名字(没有同名)各写在一张大小、形状都相同的小卡片上,并放入一个盒子里摇匀.
![]() 如果老师随便从盒子中取出一张小卡片,则每个同学被抽到的概率是多少?
如果老师随便从盒子中取出一张小卡片,则每个同学被抽到的概率是多少?
![]() 如果老师随便从盒子中抽出一张小卡片,那么抽到男同学的概率大还是抽到女同学的概率大?
如果老师随便从盒子中抽出一张小卡片,那么抽到男同学的概率大还是抽到女同学的概率大?
![]() 若老师已从盒子中抽出了
若老师已从盒子中抽出了![]() 张小卡片,其中有
张小卡片,其中有![]() 个是男同学,并把这
个是男同学,并把这![]() 张小卡片放在一边,再从盒子中抽出第
张小卡片放在一边,再从盒子中抽出第![]() 张小卡片,则这时女同学被抽到的概率是多少?
张小卡片,则这时女同学被抽到的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,A、E、F、C在同一直线上,AF=CE,过E、F分别作DE⊥AC,BF⊥AC,若AB=CD.
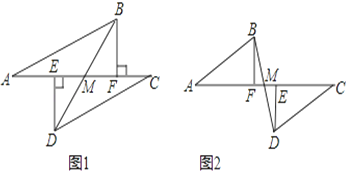
(1)试说明ME=MF.
(2)若将E、F两点移至如图2中的位置,其余条件不变,上述结论是否仍然成立?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com