
【题目】关于x的方程(k﹣1)x2+2kx+2=0.
(1)求证:无论k为何值,方程总有实数根.
(2)设x1,x2是方程(k﹣1)x2+2kx+2=0的两个根,记![]() ,S的值能为2吗?若能,求出此时k的值;若不能,请说明理由.
,S的值能为2吗?若能,求出此时k的值;若不能,请说明理由.
【答案】(1)见解析;(2) k=2
【解析】试题分析:
(1)①当k=1时,原方程是一元一次方程,其有解;②当![]() 时,原方程是一元二次方程,列出“根的判别式的表达式”,并证明其值为非负数即可可得出原方程一定有实数根;综合①②可得结论;
时,原方程是一元二次方程,列出“根的判别式的表达式”,并证明其值为非负数即可可得出原方程一定有实数根;综合①②可得结论;
(2)由原方程有两根可知:“![]() ”,根据“一元二次方程根与系数的关系”列出“两根和与两根积的表达式”代入S=2中得到关于“k”的方程,解方程求出“k”的值即可.
”,根据“一元二次方程根与系数的关系”列出“两根和与两根积的表达式”代入S=2中得到关于“k”的方程,解方程求出“k”的值即可.
试题解析:
(1)①当k=1时,原方程可化为2x+2=0,解得:x=﹣1,此时该方程有实根;
②当k≠1时,方程是一元二次方程,
∵△=(2k)2﹣4(k﹣1)×2
=4k2﹣8k+8
=4(k﹣1)2+4>0,
∴无论k为何实数,方程总有实数根;
综上所述,无论k为何实数,方程总有实数根.
(2)∵原方程有两根实数根,
∴原方程为一元二次方程, ![]() .
.
由根与系数关系可知, ![]() ,
, ![]() ,
,
若S=2,则![]() ,即
,即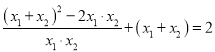 ,
,
将![]() ,
, ![]() 代入整理得:
代入整理得: ![]() ,
,
解得:k=1(舍)或k=2,
∴S的值能为2,此时k=2.


科目:初中数学 来源: 题型:
【题目】若规定两数a、b通过“※”运算,得到4ab,即a※b=4ab,例如2※6=4×2×6=48
(1)求3※5的值;
(2)求x※x+2※x-2※4=0中x的值;
(3)若无论x是什么数,总有a※x=x,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+2x+2m=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若x1,x2是一元二次方程x2+2x+2m=0的两个根,且x12+x22=8,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由7个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点.已知每个正六边形的边长为1,△ABC的顶点都在格点上,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每度生活用电的电费为0.53元,某用户5月份所交电费y(元)与这个月用电量x(度)之间的关系式为___________,若通过查电表知道x=80度,那么该用户应付电费____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三角形中,一个内角的______与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.三角形的三条角平分线________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com