
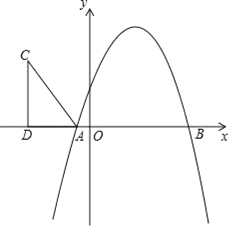
����Ŀ����ͼ��������y����x2��bx��c��x���ཻ��A����1��0����B��5��0�����㣮
��1���������ߵĽ���ʽ��
��2���ڵڶ�������ȡһ��C����CD��ֱx���ڵ�D������AC����AD��5��CD��8����Rt��ACD��x������ƽ��m����λ������C������������ʱ����m��ֵ��
��3���ڣ�2���������£�����C��һ�������������ϼ�Ϊ��E����P�������߶Գ�����һ�㣮��̽���������������Ƿ���ڵ�Q��ʹ�Ե�B��E��P��QΪ������ı�����ƽ���ı��Σ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y����x2��4x��5��2��m��ֵΪ7��9��3��Q�������Ϊ����2����7����6����7����4��5��
�����������⣨1����A��B�����꣬���ô���ϵ��������������ߵĽ���ʽ��
��2������������C�����꣬��ƽ�ƺ�ĵ�C�Ķ�Ӧ��ΪC������C�����������Ϊ8�����������߽���ʽ�����C��������꣬������ƽ�Ƶĵ�λ�������m��ֵ��
��3���ɣ�2�������E�����꣬����BE���Գ����ڵ�M����E��EF��x���ڵ�F����BEΪƽ���ı��εı�ʱ����Q���Գ���Ĵ��ߣ�����ΪN�����֤����PQN�ա�EFB�������QN���������Q���Գ���ľ��룬������Q��ĺ����꣬���������߽���ʽ�����Q�����ꣻ��BEΪ�Խ���ʱ����B��E�����������߶�BE���е����꣬��Q��x��y������P��ĺ�����������Q��ĺ����꣬���������߽���ʽ�����Q������꣮
�����������1����������y=��x2+bx+c��x��ֱ���A����1��0����B��5��0�����㣬
��![]() �����
�����![]() ��
��
�������߽���ʽΪy=��x2+4x+5��
��2����AD=5����OA=1��
��OD=6����CD=8��
��C����6��8����
��ƽ�ƺ�ĵ�C�Ķ�Ӧ��ΪC������C�����������Ϊ8��
���������߽���ʽ�ɵ�8=��x2+4x+5�����x=1��x=3��
��C�����������1��8����3��8����
��C����6��8����
������C������������ʱ������ƽ����7��9����λ��
��m��ֵΪ7��9��
��3����y=��x2+4x+5=����x��2��2+9��
�������߶Գ���Ϊx=2��
������P��2��t����
�ɣ�2����֪E������Ϊ��1��8����
����BEΪƽ���ı��εı�ʱ������BE���Գ����ڵ�M����E��EF��x���ڵ�F����BEΪƽ���ı��εı�ʱ����Q���Գ���Ĵ��ߣ�����ΪN����ͼ��
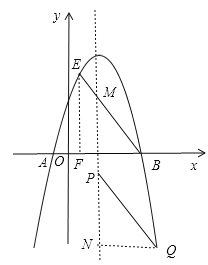
����BEF=��BMP=��QPN��
����PQN����EFB��
���PQN�ա�EFB��AAS����
��NQ=BF=OB��OF=5��1=4��
��Q��x��y������QN=|x��2|��
��|x��2|=4�����x=��2��x=6��
��x=��2��x=6ʱ�����������߽���ʽ�����y=��7��
��Q����������2����7����6����7����
����BEΪ�Խ���ʱ��
��B��5��0����E��1��8����
���߶�BE���е�����Ϊ��3��4�������߶�PQ���е�����Ϊ��3��4����
��Q��x��y������P��2��t����
��x+2=3��2�����x=4����x=4���������߽���ʽ�����y=5��
��Q��4��5����
���Ͽ�֪Q�������Ϊ����2����7����6����7����4��5����


 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P�Ǿ���ABCD�ı���һ���㣬�������߳�AB��BC���ֱ�Ϊ15��20����ôP�����������Խ���AC��BD�ľ���֮���ǣ�������
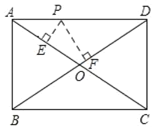
A.6B.12C.24D.����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������a��b��c����max{a��b��c}��ʾ��������������������磺max{-2��1��0}=1��max

������⣺
��1����գ�max{1��2��3}=______�����max{3��4��2x-6}=2x-6����x��ȡֵ��ΧΪ______��
��2�����max{2��x+2��-3x-7}=5����x��ֵ��
��3����ͼ����ͬһ����ϵ�л���������һ�κ�����ͼ��y=-x-3��y=x-1��y=3x-3��۲�������������ͼ��
����ͼ�л���max{-x-3��x-1��3x-3}��Ӧ��ͼ�Ӵ֣���
��max{-x-3��x-1��3x-3}����СֵΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
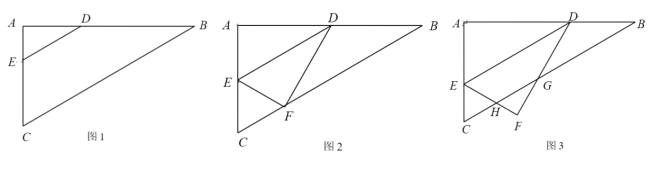
����Ŀ����֪����ͼ1����![]() �У�
��![]() ����ABC=30����
����ABC=30����![]() ����
����![]() ��E�ֱ��DZ�
��E�ֱ��DZ�![]() ��AC�϶��㣬��
��AC�϶��㣬��![]() �����
�����![]() ��
��![]() �غϣ�DE��BC��
�غϣ�DE��BC��
��1����ͼ1����AE=1ʱ����![]() ����
����
��2����ͼ2��������ֱ��![]() ���۵õ�
���۵õ�![]() ����
����![]()
�ٵ���F����б��![]() ��ʱ����
��ʱ����![]() ��ֵ��
��ֵ��
�� ��ͼ3������F����![]() �ⲿʱ��EF��DF�ֱ���
�ⲿʱ��EF��DF�ֱ���![]() �ཻ�ڵ�H��G�������ABC�͡�DEF�ص����ֵ����Ϊ
�ཻ�ڵ�H��G�������ABC�͡�DEF�ص����ֵ����Ϊ![]() ����
����![]() ��
��![]() �ĺ�����ϵʽ��������ֱ��д���𰸣�
�ĺ�����ϵʽ��������ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+c��a��0��ͼ���һ���֣��Գ���Ϊx=![]() ���Ҿ����㣨2��0����������˵������abc��0����a+b=0����4a+2b+c��0��������0��y1������1��y2�����������ϵ����㣬��y1=y2������˵����ȷ���ǣ� ��
���Ҿ����㣨2��0����������˵������abc��0����a+b=0����4a+2b+c��0��������0��y1������1��y2�����������ϵ����㣬��y1=y2������˵����ȷ���ǣ� ��

A���٢ڢ� B���ۢ� C���٢ۢ� D���٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾����Ͳ�����������ʽ��������Ա�����ʶ�ȡ�ͣ������˷����ù�˾����10�����ţ��Ҹ����ŵ�������ͬ.Ϊ�˽���͵��˷����������10�������������ȡ��![]() �������ţ��������������ܣ�20�������գ��ĵ��飬�õ�����������ÿ������˷ѷ��˵����������¼����ÿ�ղ�������������λ��ǧ�ˣ���������Щ���ݽ����������������ͷ���.��������˲�����Ϣ.
�������ţ��������������ܣ�20�������գ��ĵ��飬�õ�����������ÿ������˷ѷ��˵����������¼����ÿ�ղ�������������λ��ǧ�ˣ���������Щ���ݽ����������������ͷ���.��������˲�����Ϣ.![]() .
.![]() ����ÿ�ղ���������Ƶ���ֲ�ֱ��ͼ���£����ݷֳ�6�飺
����ÿ�ղ���������Ƶ���ֲ�ֱ��ͼ���£����ݷֳ�6�飺![]() ��
��![]() ��
��![]() ��
��![]() ����
����
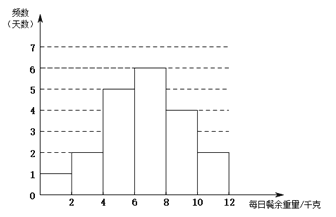
![]() .
.![]() ����ÿ�ղ���������
����ÿ�ղ���������![]() ��һ����ǣ�6.1 6.6 7.0 7.0 7.0 7.8
��һ����ǣ�6.1 6.6 7.0 7.0 7.0 7.8
![]() .
.![]() ����ÿ�ղ����������£�1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
����ÿ�ղ����������£�1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
![]() .
. ![]() ����������20��������ÿ�ղ���������ƽ��������λ�����������£�
����������20��������ÿ�ղ���������ƽ��������λ�����������£�
���� | ƽ���� | ��λ�� | ���� |
| 6.4 | | 7.0 |
| 6.6 | 7.2 | |
����������Ϣ���ش��������⣺
��1��д����![]() �е�ֵ��
�е�ֵ��
��2����![]() �����������У����ʶ�ȡ�ͣ������˷������ýϺõIJ�����________������
�����������У����ʶ�ȡ�ͣ������˷������ýϺõIJ�����________������![]() ������
������![]() ������������____________��
������������____________��
��3�����![]() ����������ÿ�ղ������������ݣ����Ƹù�˾��10�����ţ�һ�꣨��240�������ռ��㣩�IJ���������.
����������ÿ�ղ������������ݣ����Ƹù�˾��10�����ţ�һ�꣨��240�������ռ��㣩�IJ���������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ�������г��㽶�ļ۸����±�
�����㽶��(ǧ��) | ������20ǧ�� | 20ǧ�����ϵ�������40ǧ�� | 40ǧ������ |
ÿǧ�˵ļ۸� | 6Ԫ | 5Ԫ | 4Ԫ |
��ǿ���ι������㽶50ǧ��,��֪�ڶ��ι�����������ڵ�һ�ι��������,������264Ԫ,������ǿ��һ��,�ڶ��ηֱ����㽶����ǧ��?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���![]() �У�
��![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() ��
��![]() �ϣ�
�ϣ�![]() �����߶�
�����߶�![]() �Ƶ�
�Ƶ�![]() ��˳ʱ�뷽����ת
��˳ʱ�뷽����ת![]() �õ�
�õ�![]() ������
������![]() ��Ȼ���
��Ȼ���![]() ����
����![]() ���۵õ�
���۵õ�![]() ������
������![]() ��
��![]() ��ȡ
��ȡ![]() ���е�
���е�![]() ������
������![]() ����
����![]() �ij��� ��
�ij��� ��

A.![]() B.
B.![]() C.2D.
C.2D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
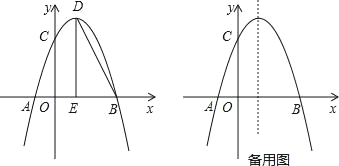
����Ŀ����ͼ��������y=��x2+bx+c��x�ύ�ڵ�A�͵�B��3��0������y�ύ�ڵ�C��0��3������D�������ߵĶ��㣬����D��x��Ĵ��ߣ�����ΪE������DB��
��1����������ߵĽ���ʽ������D�����ꣻ
��2����M���������ϵĶ��㣬���M�ĺ�����Ϊm��
������MBA=��BDEʱ�����M�����ꣻ
������M��MN��x�ᣬ�������߽��ڵ�N��PΪx����һ�㣬����PM��PN������PMN����MN���ۣ�����QMN�����ı���MPNQǡ��Ϊ�����Σ�ֱ��д��m��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com