
����Ŀ��ij��˾����Ͳ�����������ʽ��������Ա�����ʶ�ȡ�ͣ������˷����ù�˾����10�����ţ��Ҹ����ŵ�������ͬ.Ϊ�˽���͵��˷����������10�������������ȡ��![]() �������ţ��������������ܣ�20�������գ��ĵ��飬�õ�����������ÿ������˷ѷ��˵����������¼����ÿ�ղ�������������λ��ǧ�ˣ���������Щ���ݽ����������������ͷ���.��������˲�����Ϣ.
�������ţ��������������ܣ�20�������գ��ĵ��飬�õ�����������ÿ������˷ѷ��˵����������¼����ÿ�ղ�������������λ��ǧ�ˣ���������Щ���ݽ����������������ͷ���.��������˲�����Ϣ.![]() .
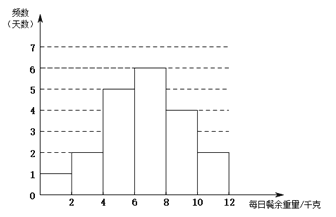
.![]() ����ÿ�ղ���������Ƶ���ֲ�ֱ��ͼ���£����ݷֳ�6�飺
����ÿ�ղ���������Ƶ���ֲ�ֱ��ͼ���£����ݷֳ�6�飺![]() ��
��![]() ��
��![]() ��
��![]() ����
����
![]() .
.![]() ����ÿ�ղ���������
����ÿ�ղ���������![]() ��һ����ǣ�6.1 6.6 7.0 7.0 7.0 7.8
��һ����ǣ�6.1 6.6 7.0 7.0 7.0 7.8
![]() .
.![]() ����ÿ�ղ����������£�1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
����ÿ�ղ����������£�1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
![]() .
. ![]() ����������20��������ÿ�ղ���������ƽ��������λ�����������£�
����������20��������ÿ�ղ���������ƽ��������λ�����������£�
���� | ƽ���� | ��λ�� | ���� |
| 6.4 | | 7.0 |
| 6.6 | 7.2 | |
����������Ϣ���ش��������⣺
��1��д����![]() �е�ֵ��
�е�ֵ��
��2����![]() �����������У����ʶ�ȡ�ͣ������˷������ýϺõIJ�����________������
�����������У����ʶ�ȡ�ͣ������˷������ýϺõIJ�����________������![]() ������
������![]() ������������____________��
������������____________��
��3�����![]() ����������ÿ�ղ������������ݣ����Ƹù�˾��10�����ţ�һ�꣨��240�������ռ��㣩�IJ���������.
����������ÿ�ղ������������ݣ����Ƹù�˾��10�����ţ�һ�꣨��240�������ռ��㣩�IJ���������.
���𰸡�(1)m=6.8��n=6.9;(2) A��A����ÿ�ղ���������ƽ��������λ����С��B����ÿ�ղ���������ƽ��������λ����3��15600kg��
��������
��1������Ƶ�����ʣ��ֲ�ֱ��ͼ�����ݼ��ɵõ����ۣ�
��2�����ݱ������ݼ��ɵõ����ۣ�
��3������A��B����������20��������ÿ�ղ�������ƽ�������ɵõ����ۣ�
��1��m=![]() =6.8��n=6.9��
=6.8��n=6.9��
��2����A��B�����������У����ʶ�ȡ�ͣ������˷������ýϺõIJ�����A��������A����ÿ�ղ���������ƽ��������λ����С��B����ÿ�ղ���������ƽ��������λ����
�ʴ�ΪA��A����ÿ�ղ���������ƽ��������λ����С��B����ÿ�ղ���������ƽ��������λ����
��3��10��240��![]() =15600kg��
=15600kg��
�𣺹��Ƹù�˾��10�����ţ�һ�꣨��240�������ռ��㣩�IJ�������15600kg��


 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д� ��У���˿��ֿ���ϵ�д�
��У���˿��ֿ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AC��BD�ཻ�ڵ�O��AEƽ����BAD����BC��E������EAO=15��������BOE�Ķ���Ϊ �ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ABC�У���B��60������M�ӵ�B����������BC����������BC���˶����ڵ�M�˶��Ĺ����У�����AM������AMΪ��������BC�Ϸ������ȱ���AMN������CN��
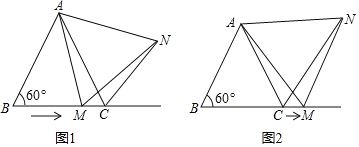
��1������BAM���� ����ʱ��AB��2BM��
��2��������һ���������� ����ʹ����ABCΪ�ȱ������Σ�
����ͼ1������ABCΪ�ȱ�������ʱ����֤��CN+CM��AC��
����ͼ2������M�˶����߶�BC֮�⣨����M���߶�BC���ӳ�����ʱ���������������䣨��ABC��Ϊ�ȱ������Σ�����д����ʱ�߶�CN��CM��AC�����������ϵ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
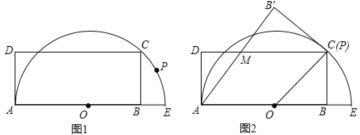
����Ŀ����ͼ1����֪��AEΪֱ���İ�ԲԲ��ΪO���뾶Ϊ5������ABCD�Ķ���B��ֱ��AE�ϣ�����C �ڰ�Բ�ϣ�AB=8����PΪ��Բ��һ�㣨����A��E�����غϣ���
��1������ABCD�ı�BC�ij�Ϊ���٣�
��2����������ֱ��AP�۵�����B���ڵ�B�䣮
�ٵ�B�䵽ֱ��AE���������Ƕ��٣�
�ڵ���P���C�غ�ʱ����ͼ2��ʾ��AB�佻DC�ڵ�M��
��֤���ı���AOCM�����Σ���ͨ��֤���ж�CB�����Բ��λ�ù�ϵ��
�۵�EB���BDʱ��ֱ��д��EB��ij�Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
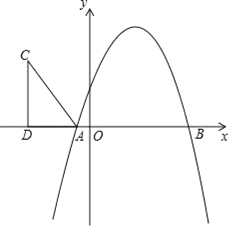
����Ŀ����ͼ��������y����x2��bx��c��x���ཻ��A����1��0����B��5��0�����㣮
��1���������ߵĽ���ʽ��
��2���ڵڶ�������ȡһ��C����CD��ֱx���ڵ�D������AC����AD��5��CD��8����Rt��ACD��x������ƽ��m����λ������C������������ʱ����m��ֵ��
��3���ڣ�2���������£�����C��һ�������������ϼ�Ϊ��E����P�������߶Գ�����һ�㣮��̽���������������Ƿ���ڵ�Q��ʹ�Ե�B��E��P��QΪ������ı�����ƽ���ı��Σ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������y=ax2+bx+c��������ֱ��ڵ�A��0��6����B��6��0����C����2��0������P���߶�AB�Ϸ��������ϵ�һ�����㣮
��1���������ߵĽ���ʽ��
��2������P�˶���ʲôλ��ʱ����PAB����������ֵ��
��3������P��x��Ĵ��ߣ����߶�AB�ڵ�D���ٹ���P��PE��x�ύ�������ڵ�E������DE�������Ƿ���ڵ�Pʹ��PDEΪ����ֱ�������Σ������ڣ������P�����ꣻ�������ڣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������20�����ˣ�ijһ�������������������ͳ�����±���
��������ĸ���(��) | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
��������(��) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
��1������һ��20���������������ƽ��������
��2��Ϊ����ߴ�������˵Ļ����ԣ���������ʵ�С�ÿ�춨�������������н����Ĵ�ʩ.������ǹ����ߣ���ƽ��������λ���������ĽǶȽ��з������㽫���ȷ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʮ�£�����Ʈ�㣬����˫��������ѧӭ��������֪���¿Ƽ������������꼶ij���18�˱����μӺ����飬����������˻���������Ŀ��ı�����ÿ���μ�һ������к������ͬѧ�����˻����ͬѧ��������3�ˣ��������ͬѧ������3�˵�������9�ˣ��༶����Ϊ�������ÿλͬѧ����2������ģ�ͣ�Ϊ�������ÿλͬѧ����3������ģ�ͣ�Ϊ���˻����ÿλͬѧ�������ɸ����˻�ģ�ͣ���֪����ģ��75Ԫÿ��������ģ��98Ԫÿ�������˻�ģ��165Ԫÿ����������������ģ���軨��6114Ԫ�������й������˻�ģ�͵ķ�����__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ⱳ����
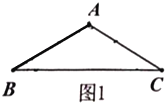
��1����ͼ1������![]() �У�
��![]() ��
��![]() ����
����![]() ______��
______��
��֪ʶӦ�ã�
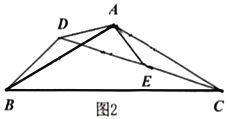
��2����ͼ2��![]() ��
��![]() ���ǵ��������Σ�
���ǵ��������Σ�![]() ��
��![]() ��
��![]() ��
��![]() ������ͬһ��ֱ���ϣ�����
������ͬһ��ֱ���ϣ�����![]() .
.
����֤��![]() ��
��
����д���߶�![]() ��
��![]() ��
��![]() ֮��ĵ�����ϵʽ����˵�����ɣ�
֮��ĵ�����ϵʽ����˵�����ɣ�
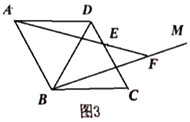
��3����ͼ3��![]() ��
��![]() ��Ϊ�ȱ������Σ���
��Ϊ�ȱ������Σ���![]() ��������
��������![]() ������
������![]() ����
����![]() �ĶԳƵ�
�ĶԳƵ�![]() ������
������![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() .��
.��![]() ��
��![]() ����
����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com