
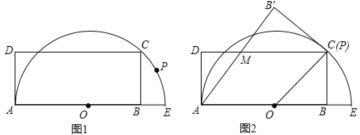
【题目】如图1,已知以AE为直径的半圆圆心为O,半径为5,矩形ABCD的顶点B在直径AE上,顶点C 在半圆上,AB=8,点P为半圆上一点(不与A、E两点重合).
(1)矩形ABCD的边BC的长为多少;
(2)将矩形沿直线AP折叠,点B落在点B′.
①点B′到直线AE的最大距离是多少;
②当点P与点C重合时,如图2所示,AB′交DC于点M.
求证:四边形AOCM是菱形,并通过证明判断CB′与半圆的位置关系;
③当EB′∥BD时,直接写出EB′的长为多少.
【答案】(1)4;(2)①8;②见解析;(3)满足条件的EB′的长为4![]() +2
+2![]() 或4
或4![]() -2
-2![]() .
.
【解析】
(1)图1中,在Rt△OBC中,求出BC即可;
(2)①图1中,当点B′在直线AD上时,点B'到AE的距离最大,最大距离为8;②首先证明四边形AOCM是平行四边形,由OA=OC即可判定四边形AOCM是菱形.只要证明∠OCB′=90°即可判定CB′与半圆相切;③图3中,当EB′∥BD时,作AF⊥EB′于F.由△AEF∽△DBA,可得![]() =
=![]() =
=![]() ,推出EF=4
,推出EF=4![]() ,AF=2
,AF=2![]() ,在Rt△AFB′中,FB′=
,在Rt△AFB′中,FB′=![]() =2
=2![]() ,即可推出EB′=4
,即可推出EB′=4![]() +2
+2![]() .图4中,当EB′∥BD时,作AF⊥EB′于F,同法可求EB′.
.图4中,当EB′∥BD时,作AF⊥EB′于F,同法可求EB′.
(1)如图1中,连接OC,

在Rt△BOC中,∵∠OBC=90°,OC=5,OB=3,
∴BC=![]() ;
;
(2)①如图1中,当点B′在直线AD上时,点B'到AE的距离最大,最大距离为8.
②证明:

由折叠可知:∠OAC=∠MAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠OCA=∠MAC,
∴OC∥AM,
又∵CM∥OA,
∴四边形AOCM是平行四边形,
又∵OA=OC,
∴□AOCM是菱形;
结论:CB′与半圆相切,
理由:由折叠可知:∠ABˊC=∠ABC=90°,
∵OC∥AM,
∴∠ABˊC+∠BˊCO=180°,
∴∠BˊCO=90°,
∴CBˊ⊥OC,
∴CBˊ与半圆相切;
③如图3中,当EB′∥BD时,作AF⊥EB′于F,

由△AEF∽△DBA,
∴,
∴EF=4![]() ,AF=2
,AF=2![]() ,
,
在Rt△AFB′中,FB′=![]() ,
,
∴EB′=4![]() +2
+2![]() ,
,
如图4中,当EB′∥BD时,作AF⊥EB′于F,

同法可得EF=4![]() ,FB′=2
,FB′=2![]() ,
,
∴EB′=4![]() -2
-2![]() .
.
综上所述,满足条件的EB′的长为4![]() +2
+2![]() 或4
或4![]() -2
-2![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】我校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 | 正确数字x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息解决下列问题:
(1)在统计表中,m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)有三位评委老师,每位老师在E组学生完成学校比赛后,出示“通过”或“淘汰”或“待定”的评定结果.学校规定:每位学生至少获得两位评委老师的“通过”才能代表学校参加鄂州市“汉字听写”比赛,请用树形图求出E组学生王云参加鄂州市“汉字听写”比赛的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
(1)若∠A=40°,求∠DBC的度数.
(2)若△BCD的周长为16cm,△ABC的周长为26cm,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是A(1,3),B(﹣2,﹣2),C(2,﹣1).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)写出点A1,B1,C1的坐标;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
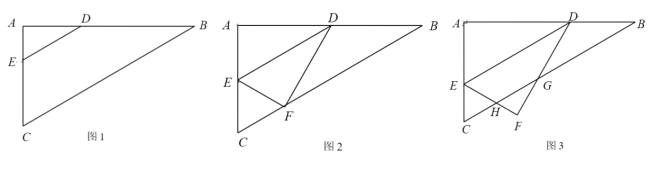
【题目】已知:如图1,在![]() 中,
中,![]() ,∠ABC=30°,
,∠ABC=30°,![]() ,点
,点![]() 、E分别是边
、E分别是边![]() 、AC上动点,点
、AC上动点,点![]() 不与点
不与点![]() 、
、![]() 重合,DE∥BC.
重合,DE∥BC.
(1)如图1,当AE=1时,求![]() 长;
长;
(2)如图2,把沿着直线![]() 翻折得到
翻折得到![]() ,设
,设![]()
①当点F落在斜边![]() 上时,求
上时,求![]() 的值;
的值;
② 如图3,当点F落在![]() 外部时,EF、DF分别与
外部时,EF、DF分别与![]() 相交于点H、G,如果△ABC和△DEF重叠部分的面积为
相交于点H、G,如果△ABC和△DEF重叠部分的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式及定义域.(直接写出答案)
的函数关系式及定义域.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果抛物线y=ax2+bx+c过定点M(1,0),则称此抛物线为定点抛物线.
(1)张老师在投影屏幕上出示了一个题目:请你写出一条定点抛物线的解析式.小敏写出了一个正确的答案:y=2x2+3x-5.请你写出一个不同于小敏的答案;
(2)张老师又在投影屏幕上出示了一个思考题:已知定点抛物线y=-x2+2bx+c,求该抛物线的顶点最低时的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司的午餐采用自助的形式,并倡导员工“适度取餐,减少浪费”该公司共有10个部门,且各部门的人数相同.为了解午餐的浪费情况,从这10个部门中随机抽取了![]() 两个部门,进行了连续四周(20个工作日)的调查,得到这两个部门每天午餐浪费饭菜的重量,以下简称“每日餐余重量”(单位:千克),并对这些数据进行了整理、描述和分析.下面给出了部分信息.
两个部门,进行了连续四周(20个工作日)的调查,得到这两个部门每天午餐浪费饭菜的重量,以下简称“每日餐余重量”(单位:千克),并对这些数据进行了整理、描述和分析.下面给出了部分信息.![]() .
.![]() 部门每日餐余重量的频数分布直方图如下(数据分成6组:
部门每日餐余重量的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ):
):
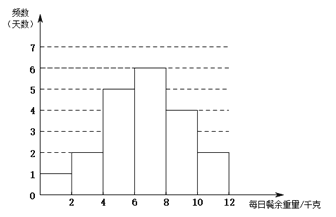
![]() .
.![]() 部门每日餐余重量在
部门每日餐余重量在![]() 这一组的是:6.1 6.6 7.0 7.0 7.0 7.8
这一组的是:6.1 6.6 7.0 7.0 7.0 7.8
![]() .
.![]() 部门每日餐余重量如下:1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
部门每日餐余重量如下:1.4 2.8 6.9 7.8 1.9 9.7 3.1 4.6 6.9 10.8 6.9 2.6 7.5 6.9 9.5 7.8 8.4 8.3 9.4 8.8
![]() .
. ![]() 两个部门这20个工作日每日餐余重量的平均数、中位数、众数如下:
两个部门这20个工作日每日餐余重量的平均数、中位数、众数如下:
部门 | 平均数 | 中位数 | 众数 |
| 6.4 | | 7.0 |
| 6.6 | 7.2 | |
根据以上信息,回答下列问题:
(1)写出表![]() 中的值;
中的值;
(2)在![]() 这两个部门中,“适度取餐,减少浪费”做得较好的部门是________(填“
这两个部门中,“适度取餐,减少浪费”做得较好的部门是________(填“![]() ”或“
”或“![]() ”),理由是____________;
”),理由是____________;
(3)结合![]() 这两个部门每日餐余重量的数据,估计该公司(10个部门)一年(按240个工作日计算)的餐余总重量.
这两个部门每日餐余重量的数据,估计该公司(10个部门)一年(按240个工作日计算)的餐余总重量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数![]() 和
和![]() 的图象关于原点成中心对称,我们就称其中一个函数是另一个函数的中心对称函数,也称函数
的图象关于原点成中心对称,我们就称其中一个函数是另一个函数的中心对称函数,也称函数![]() 和
和![]() 互为中心对称函数.
互为中心对称函数.
![]() 求函数
求函数![]() 的中心对称函数;
的中心对称函数;
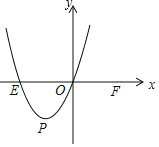
![]() 如图,在平面直角坐标系xOy中,E,F两点的坐标分别为
如图,在平面直角坐标系xOy中,E,F两点的坐标分别为![]() ,
,![]() ,二次函数
,二次函数![]() 的图象经过点E和原点O,顶点为
的图象经过点E和原点O,顶点为![]() 已知函数
已知函数![]() 和
和![]() 互为中心对称函数;
互为中心对称函数;
![]() 请在图中作出二次函数
请在图中作出二次函数![]() 的顶点
的顶点![]() 作图工具不限
作图工具不限![]() ,并画出函数
,并画出函数![]() 的大致图象;
的大致图象;
![]() 当四边形EPFQ是矩形时,请求出a的值;
当四边形EPFQ是矩形时,请求出a的值;
![]() 已知二次函数
已知二次函数![]() 和
和![]() 互为中心对称函数,且
互为中心对称函数,且![]() 的图象经过
的图象经过![]() 的顶点当
的顶点当![]() 时,求代数式
时,求代数式![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例y=![]() 的图象与一次函数y=kx﹣3的图象在第一象限内交于A(4,a).
的图象与一次函数y=kx﹣3的图象在第一象限内交于A(4,a).
(1)求一次函数的解析式;
(2)若直线x=n(0<n<4)与反比例函数和一次函数的图象分别交于点B,C,连接AB,若△ABC是等腰直角三角形,求n的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com