
����Ŀ�������κ���![]() ��
��![]() ��ͼ�����ԭ������ĶԳƣ����Ǿͳ�����һ����������һ�����������ĶԳƺ�����Ҳ�ƺ���
��ͼ�����ԭ������ĶԳƣ����Ǿͳ�����һ����������һ�����������ĶԳƺ�����Ҳ�ƺ���![]() ��
��![]() ��Ϊ���ĶԳƺ�����
��Ϊ���ĶԳƺ�����
![]() ����
����![]() �����ĶԳƺ�����
�����ĶԳƺ�����
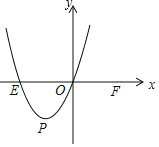
![]() ��ͼ����ƽ��ֱ������ϵxOy�У�E��F���������ֱ�Ϊ
��ͼ����ƽ��ֱ������ϵxOy�У�E��F���������ֱ�Ϊ![]() ��
��![]() �������
�����κ���![]() ��ͼ����E��ԭ��O������Ϊ
��ͼ����E��ԭ��O������Ϊ![]() ��֪����
��֪����![]() ��
��![]() ��Ϊ���ĶԳƺ�����
��Ϊ���ĶԳƺ�����
![]() ����ͼ���������κ���
����ͼ���������κ���![]() �Ķ���
�Ķ���![]() ��ͼ���߲���
��ͼ���߲���![]() ������������
������������![]() �Ĵ���ͼ��
�Ĵ���ͼ��
![]() ���ı���EPFQ�Ǿ���ʱ�������a��ֵ��
���ı���EPFQ�Ǿ���ʱ�������a��ֵ��
![]() ��֪���κ���
��֪���κ���![]() ��
��![]() ��Ϊ���ĶԳƺ�������
��Ϊ���ĶԳƺ�������![]() ��ͼ��
��ͼ��![]() �Ķ��㵱
�Ķ��㵱![]() ʱ�������ʽ
ʱ�������ʽ![]() �����ֵ��
�����ֵ��
���𰸡�![]() ��
��![]() ��ͼ��������
��ͼ��������![]() a��ֵΪ
a��ֵΪ![]() ��
��![]() ��
��![]() ʱ��
ʱ��![]() �����ֵ�����ֵΪ3��
�����ֵ�����ֵΪ3��
��������
![]() �����䷽���õ�
�����䷽���õ�![]() ����������ߵĶ�������Ϊ
����������ߵĶ�������Ϊ![]() ���������ĶԳƵ����ʵõ�
���������ĶԳƵ����ʵõ�![]() ����ԭ��ԳƵĵ������Ϊ
����ԭ��ԳƵĵ������Ϊ![]() ��Ȼ�����ö���ʽд������
��Ȼ�����ö���ʽд������![]() �����ĶԳƺ�������ʽ��
�����ĶԳƺ�������ʽ��
![]() ��P�����ԭ��ĶԳƵ�õ�q�㣬Ȼ����»�������ΪQ������ԭ���F��������ߣ�
��P�����ԭ��ĶԳƵ�õ�q�㣬Ȼ����»�������ΪQ������ԭ���F��������ߣ�
![]() ���þ��ε����ʵ�
���þ��ε����ʵ�![]() �������������ߵĶԳ��Եõ�
�������������ߵĶԳ��Եõ�![]() ������ж�
������ж�![]() Ϊ�ȱ������Σ���
Ϊ�ȱ������Σ���![]() ��H����ͼ����
��H����ͼ����![]() ��
��![]() ������
������![]() ���轻��ʽ
���轻��ʽ![]() ��Ȼ���P��������뼴�ɵõ�a��ֵ��
��Ȼ���P��������뼴�ɵõ�a��ֵ��
![]() ��
��![]() ��Ϊ����ʽ�õ�������
��Ϊ����ʽ�õ�������![]() �Ķ�������Ϊ
�Ķ�������Ϊ![]() �����ù���ԭ��ԳƵĵ�����������õ�������
�����ù���ԭ��ԳƵĵ�����������õ�������![]() �Ķ�������Ϊ
�Ķ�������Ϊ![]() ���ٰ�
���ٰ�![]() ����
����![]() ��
��![]() ������
������![]() ��Ȼ�����ö��κ��������ʽ�����⣮
��Ȼ�����ö��κ��������ʽ�����⣮
![]() ��
��
![]() �������ߵĶ�������Ϊ
�������ߵĶ�������Ϊ![]() ��
��
![]() ��
��![]() ����ԭ��ԳƵĵ������Ϊ
����ԭ��ԳƵĵ������Ϊ![]() ��
��
![]() ����
����![]() �����ĶԳƺ���Ϊ
�����ĶԳƺ���Ϊ![]() ����
����![]() ��
��
![]() ��ͼ��
��ͼ��
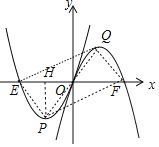
![]() �ı���EPFGΪ���Σ�
�ı���EPFGΪ���Σ�
![]() ��
��
��![]() ��
��
![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�
��![]() ��H����ͼ��
��H����ͼ��
��![]() ��
��![]() ��
��
![]() ��
��
����κ���![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
��![]() �����
�����![]() �����
�����![]() ��
��
��a��ֵΪ![]() ��
��
![]() ��
��
![]() ������
������![]() �Ķ�������Ϊ
�Ķ�������Ϊ![]() ��
��
![]() ������
������![]() �Ķ�����������
�Ķ�����������![]() �Ķ������ԭ��Գƣ�
�Ķ������ԭ��Գƣ�
![]() ������
������![]() �Ķ�������Ϊ
�Ķ�������Ϊ![]() ��
��
��![]() ����
����![]() ��
��![]() �����
�����![]() ��
��
![]() ��
��
��![]() ʱ��
ʱ��![]() �����ֵ�����ֵΪ3��
�����ֵ�����ֵΪ3��


 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
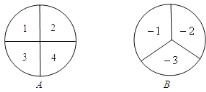
����Ŀ��С����С��������ȥ�������ᣬ����ֻ��һ����Ʊ��˭����ȥ������̶�ͨ��ת����Ϸ������������������ͼ![]() ��ʾ������������ת����ת��
��ʾ������������ת����ת��![]() ��
��![]() ��ÿ��ת�̱��ֳ������ȵļ������Σ�����ÿһ�������ڱ������֣���Ϸ�����ǣ�ͬʱת������ת�̣���ת��ֹͣ��ָ����ָ���������֮��Ϊ
��ÿ��ת�̱��ֳ������ȵļ������Σ�����ÿһ�������ڱ������֣���Ϸ�����ǣ�ͬʱת������ת�̣���ת��ֹͣ��ָ����ָ���������֮��Ϊ![]() ʱ��С��ȥ������֮��Ϊ
ʱ��С��ȥ������֮��Ϊ![]() ʱ��С��ȥ�������ָ��ǡ��ָ�ڷָ����ϣ���ô��תһ�Σ�ֱ��ָ��ָ��ijһ����Ϊֹ��
ʱ��С��ȥ�������ָ��ǡ��ָ�ڷָ����ϣ���ô��תһ�Σ�ֱ��ָ��ָ��ijһ����Ϊֹ��
![]() ����״ͼ���б�����С��ȥ�ĸ��ʣ�
����״ͼ���б�����С��ȥ�ĸ��ʣ�
![]() �����Ϸ�����С����С��˫����ƽ�����жϲ�˵�����ɣ�
�����Ϸ�����С����С��˫����ƽ�����жϲ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
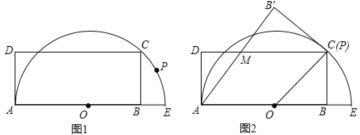
����Ŀ����ͼ1����֪��AEΪֱ���İ�ԲԲ��ΪO���뾶Ϊ5������ABCD�Ķ���B��ֱ��AE�ϣ�����C �ڰ�Բ�ϣ�AB=8����PΪ��Բ��һ�㣨����A��E�����غϣ���
��1������ABCD�ı�BC�ij�Ϊ���٣�
��2����������ֱ��AP�۵�����B���ڵ�B�䣮
�ٵ�B�䵽ֱ��AE���������Ƕ��٣�
�ڵ���P���C�غ�ʱ����ͼ2��ʾ��AB�佻DC�ڵ�M��
��֤���ı���AOCM�����Σ���ͨ��֤���ж�CB�����Բ��λ�ù�ϵ��
�۵�EB���BDʱ��ֱ��д��EB��ij�Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������y=ax2+bx+c��������ֱ��ڵ�A��0��6����B��6��0����C����2��0������P���߶�AB�Ϸ��������ϵ�һ�����㣮
��1���������ߵĽ���ʽ��
��2������P�˶���ʲôλ��ʱ����PAB����������ֵ��
��3������P��x��Ĵ��ߣ����߶�AB�ڵ�D���ٹ���P��PE��x�ύ�������ڵ�E������DE�������Ƿ���ڵ�Pʹ��PDEΪ����ֱ�������Σ������ڣ������P�����ꣻ�������ڣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������20�����ˣ�ijһ�������������������ͳ�����±���
��������ĸ���(��) | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
��������(��) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
��1������һ��20���������������ƽ��������
��2��Ϊ����ߴ�������˵Ļ����ԣ���������ʵ�С�ÿ�춨�������������н����Ĵ�ʩ.������ǹ����ߣ���ƽ��������λ���������ĽǶȽ��з������㽫���ȷ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
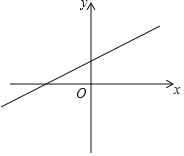
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�ֱ��l��y=![]() x+m��x���ڵ�A�����κ���y=ax2��3ax+c��a��0����a��c�dz�������ͼ����x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����ֱ��l���ڵ�D����֪CD��x��ƽ�У���S��ACD��S��ABD=3��5��
x+m��x���ڵ�A�����κ���y=ax2��3ax+c��a��0����a��c�dz�������ͼ����x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C����ֱ��l���ڵ�D����֪CD��x��ƽ�У���S��ACD��S��ABD=3��5��
��1�����A�����ꣻ
��2����˶��κ����Ľ���ʽ��
��3����PΪֱ��l��һ���㣬���߶�AC�Ƶ�P˳ʱ����ת���㣨0�㣼���㣼360�㣩�õ��߶�A'C'����A��A'�Ƕ�Ӧ�㣬��C��C'�Ƕ�Ӧ�㣩�����ʣ��Ƿ���������ĵ�P��ʹ����ת���A'�͵�C'�ֱ�����ֱ��l��������y=ax2��3ax+c��ͼ���ϣ������ڣ���ֱ��д����A'�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʮ�£�����Ʈ�㣬����˫��������ѧӭ��������֪���¿Ƽ������������꼶ij���18�˱����μӺ����飬����������˻���������Ŀ��ı�����ÿ���μ�һ������к������ͬѧ�����˻����ͬѧ��������3�ˣ��������ͬѧ������3�˵�������9�ˣ��༶����Ϊ�������ÿλͬѧ����2������ģ�ͣ�Ϊ�������ÿλͬѧ����3������ģ�ͣ�Ϊ���˻����ÿλͬѧ�������ɸ����˻�ģ�ͣ���֪����ģ��75Ԫÿ��������ģ��98Ԫÿ�������˻�ģ��165Ԫÿ����������������ģ���軨��6114Ԫ�������й������˻�ģ�͵ķ�����__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��

![]() ��˵��
��˵��![]() �����ɣ�
�����ɣ�
��2��![]() ���Ծ���ͼ�εı任�õ�
���Ծ���ͼ�εı任�õ�![]() ��������������任��
��������������任��
![]() ��
��![]() �Ķ�����
�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������![]() ��һ�κ���y=x+b��ͼ��������A��1��2��
��һ�κ���y=x+b��ͼ��������A��1��2��

��1����ȷ��������������һ�κ����Ľ���ʽ��
��2����һ�κ���ͼ������������Ľ������꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com