
【题目】如图,平面直角坐标系中,直线l:y=![]() x+m交x轴于点A,二次函数y=ax2﹣3ax+c(a≠0,且a、c是常数)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,与直线l交于点D,已知CD与x轴平行,且S△ACD:S△ABD=3:5.
x+m交x轴于点A,二次函数y=ax2﹣3ax+c(a≠0,且a、c是常数)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,与直线l交于点D,已知CD与x轴平行,且S△ACD:S△ABD=3:5.
(1)求点A的坐标;
(2)求此二次函数的解析式;
(3)点P为直线l上一动点,将线段AC绕点P顺时针旋转α°(0°<α°<360°)得到线段A'C'(点A,A'是对应点,点C,C'是对应点).请问:是否存在这样的点P,使得旋转后点A'和点C'分别落在直线l和抛物线y=ax2﹣3ax+c的图象上?若存在,请直接写出点A'的坐标;若不存在,请说明理由.
【答案】(1) A(﹣1,0);(2) y=﹣![]() (x+1)(x﹣4)=﹣
(x+1)(x﹣4)=﹣![]() x2+
x2+![]() x+2;(3)见解析.
x+2;(3)见解析.
【解析】
(1)由题意可得C(0,c),且CD∥x轴,可得D(3,c),根据面积比可得AB=5.由对称性可得点A(-2m,0)到对称轴的距离2倍是5,可求m,即可求A点坐标.
(2)由直线l过D点可求D(3,2),由A,B关于对称轴对称可求B(4,0),则可用交点式求二次函数的解析式.
(3)由点A是直线l上一点,绕直线l上点P旋转,且落在直线l上,因此可得点A与点A'重合,或点A绕点P旋转180°得到A'.设C'(a,-![]() a2+
a2+![]() a+2)根据中点坐标公式可求A'点坐标.
a+2)根据中点坐标公式可求A'点坐标.
解:(1)
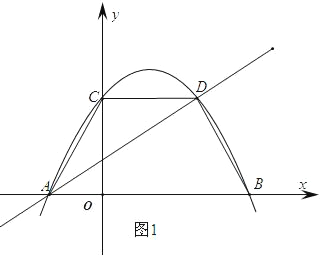
∵二次函数y=ax2﹣3ax+c(a≠0,且a、c是常数)的图象与x轴交于A、B两点
∴C(0,c,),对称轴是直线x=![]() =
=![]() .
.
∵CD∥x轴.
∴C,D关于对称轴直线x=![]() 对称.
对称.
∴D(3,c).
∵S△ACD:S△ABD=3:5.且△ACD和△ABD是等高的.
∴![]() .
.
∴AB=5.
∵直线y=![]() x+m与x轴交于A点,
x+m与x轴交于A点,
∴A(﹣2m,0).
∵点A,点B关于对称轴x=![]() 对称.
对称.
∴2×[![]() ﹣(﹣2m)]=5.
﹣(﹣2m)]=5.
∴m=![]() .
.
∴A(﹣1,0),且AB=5.
∴B(4,0).
(2)设抛物线解析式y=a(x+1)(x﹣4).
∵m=![]() .
.
∴直线AD解析式y=![]() x+
x+![]() .
.
∵D(3,c)在直线AD上.
∴c=![]() +
+![]() =2.
=2.
∴D(3,2)且在抛物线上.
∴2=a(3+1)(3﹣4).
∴a=﹣![]() .
.
∴抛物线解析式y=﹣![]() (x+1)(x﹣4)=﹣
(x+1)(x﹣4)=﹣![]() x2+
x2+![]() x+2.
x+2.
(3)∵点A在直线l上,旋转后A'点落在直线l上,
∴点A与点A'重合,或者点A绕着点P旋转180°.
当点A与点A'重合时,A'(﹣1,0).
当点A绕着点P旋转180°得到A',点C绕着点P旋转180°得到C'
∴AP=A'P,CP=CP'.
如图2:
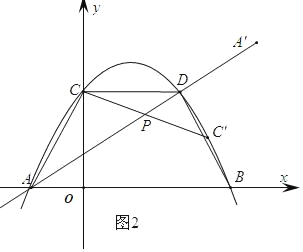
设C'(a,﹣![]() a2+
a2+![]() a+2).
a+2).
∵C( 0,2),CP=CP'.
∴P(![]() a,﹣
a,﹣![]() a2+
a2+![]() a+2).
a+2).
∵点P在直线l上,
∴﹣![]() a2+
a2+![]() a+2=
a+2=![]() a+
a+![]() .
.
即 a2﹣2a﹣6=0.
解得:a1=1+![]() ,a2=1﹣
,a2=1﹣![]() .
.
当a1=1+![]() 时,y=
时,y=![]() ×
×![]() (1+
(1+![]() )+
)+![]() =
=![]() .
.
∴P(![]() ,
,![]() ).
).
∵AP=A'P.
∴A'(2+![]() ,
,![]() ).
).
当a2=1﹣![]() 时,y=
时,y=![]() ×
×![]() (1﹣
(1﹣![]() )+
)+![]() =
=![]() .
.
∴P(![]() ,
,![]() ).
).
∵AP=AP'.
∴A'(2﹣![]() ,
,![]() ).
).
综上所述A'(2﹣![]() ,
,![]() ),(2+
),(2+![]() ,
,![]() ),(﹣1,0).
),(﹣1,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明、小刚和小红打算各自随机选择本周日的上午或下午去扬州马可波罗花世界游玩.
![]() 小明和小刚都在本周日上午去游玩的概率为________;
小明和小刚都在本周日上午去游玩的概率为________;
![]() 求他们三人在同一个半天去游玩的概率.
求他们三人在同一个半天去游玩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果抛物线y=ax2+bx+c过定点M(1,0),则称此抛物线为定点抛物线.
(1)张老师在投影屏幕上出示了一个题目:请你写出一条定点抛物线的解析式.小敏写出了一个正确的答案:y=2x2+3x-5.请你写出一个不同于小敏的答案;
(2)张老师又在投影屏幕上出示了一个思考题:已知定点抛物线y=-x2+2bx+c,求该抛物线的顶点最低时的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
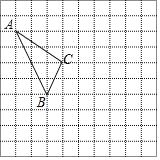
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;并写出B点坐标;
(2)请作出△ABC关于y轴对称的△A'B'C';
(3)请作出将△ABC向下平移的3个单位,再向右平移5个单位后的△A1B1C1;则点A1的坐标为_____;点B1的坐标为______,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数![]() 和
和![]() 的图象关于原点成中心对称,我们就称其中一个函数是另一个函数的中心对称函数,也称函数
的图象关于原点成中心对称,我们就称其中一个函数是另一个函数的中心对称函数,也称函数![]() 和
和![]() 互为中心对称函数.
互为中心对称函数.
![]() 求函数
求函数![]() 的中心对称函数;
的中心对称函数;
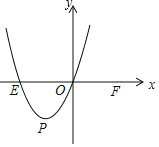
![]() 如图,在平面直角坐标系xOy中,E,F两点的坐标分别为
如图,在平面直角坐标系xOy中,E,F两点的坐标分别为![]() ,
,![]() ,二次函数
,二次函数![]() 的图象经过点E和原点O,顶点为
的图象经过点E和原点O,顶点为![]() 已知函数
已知函数![]() 和
和![]() 互为中心对称函数;
互为中心对称函数;
![]() 请在图中作出二次函数
请在图中作出二次函数![]() 的顶点
的顶点![]() 作图工具不限
作图工具不限![]() ,并画出函数
,并画出函数![]() 的大致图象;
的大致图象;
![]() 当四边形EPFQ是矩形时,请求出a的值;
当四边形EPFQ是矩形时,请求出a的值;
![]() 已知二次函数
已知二次函数![]() 和
和![]() 互为中心对称函数,且
互为中心对称函数,且![]() 的图象经过
的图象经过![]() 的顶点当
的顶点当![]() 时,求代数式
时,求代数式![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
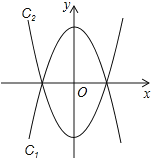
【题目】将抛物线c1: ![]() 沿x轴翻折,得到抛物线c2,如图1所示.
沿x轴翻折,得到抛物线c2,如图1所示.
(1)请直接写出抛物线c2的表达式;
(2)现将抛物线c1向左平移m个单位长度,平移后得到新抛物线的顶点为M,与x轴的交点从左到右依次为A、B;将抛物线c2向右也平移m个单位长度,平移后得到新抛物线的顶点为N,与![]() 轴的交点从左到右依次为D、E.
轴的交点从左到右依次为D、E.
①当B、D是线段AE的三等分点时,求m的值;
②在平移过程中,是否存在以点A、N、E、M为顶点的四边形是矩形的情形?若存在,请求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
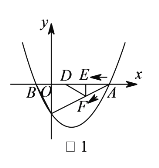
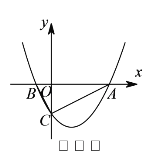
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,且当
,且当![]() 和
和![]() 时二次函数的函数值
时二次函数的函数值![]() 相等.
相等.
(![]() )求实数
)求实数![]() 、
、![]() 的值.
的值.
(![]() )如图
)如图![]() ,动点
,动点![]() 、
、![]() 同时从
同时从![]() 点出发,其中点
点出发,其中点![]() 以每秒
以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 边向终点
边向终点![]() 运动,点
运动,点![]() 以每秒
以每秒![]() 个单位长度的速度沿射线
个单位长度的速度沿射线![]() 方向运动,当点
方向运动,当点![]() 停止运动时,点
停止运动时,点![]() 随之停止运动.设运动时间为
随之停止运动.设运动时间为![]() 秒.连接
秒.连接![]() ,将
,将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在点
落在点![]() 处,得到
处,得到![]() .
.
①是否存在某一时刻![]() ,使得
,使得![]() 为直角三角形?若存在,求出
为直角三角形?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
②设![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,剪两张对边平行且宽度相等的纸条随意交叉叠放在一起,转动其中一张,重合部分构成一个四边形,则下列结论中不一定成立的是( )

A. ∠ABC=∠ADC,∠BAD=∠BCD B. AB=BC
C. AB=CD,AD=BC D. ∠DAB+∠BCD=180°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com