
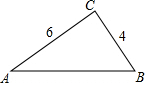
 如图,在Rt△ABC中,∠C=90°,求cosA和tanB的值.
如图,在Rt△ABC中,∠C=90°,求cosA和tanB的值. 科目:初中数学 来源: 题型:选择题
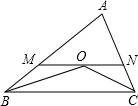 如图,△ABC中,∠ABC、∠ACB的平分线相交于O,MN过点O且与BC平行.△ABC的周长为20,△AMN的周长为12,则BC的长为( )
如图,△ABC中,∠ABC、∠ACB的平分线相交于O,MN过点O且与BC平行.△ABC的周长为20,△AMN的周长为12,则BC的长为( )| A. | 10 | B. | 16 | C. | 8 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,一棵8米高的笔直的杉树在台风中被刮断,树顶C落在离树根B点4米处,科研人员要查看断痕A处的情况,在离树根B点1米的D处竖起一个梯子AD(点D、B、C在同一直线上),请问:这个梯子有多长?(结果请保留根号)
如图所示,一棵8米高的笔直的杉树在台风中被刮断,树顶C落在离树根B点4米处,科研人员要查看断痕A处的情况,在离树根B点1米的D处竖起一个梯子AD(点D、B、C在同一直线上),请问:这个梯子有多长?(结果请保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com