
【题目】如图 ![]() ,已知
,已知![]() 中,AB=BC,
中,AB=BC,![]() ,点
,点 ![]() 为斜边
为斜边 ![]() 的中点,连接
的中点,连接 ![]() ,AF是
,AF是 ![]() 的平分线,分别与 BD、
的平分线,分别与 BD、![]() 相交于点 E、F.
相交于点 E、F.

(1)求证:![]() ;
;
(2)如图![]() ,连接
,连接 ![]() ,在不添加任何辅助线的条件下,直接写出图中所有的等腰三角形(不包含
,在不添加任何辅助线的条件下,直接写出图中所有的等腰三角形(不包含![]() ).
).
【答案】(1)详见解析;(2)(2)△ABD、△CBD 、△ECA、△BEF是等腰三角形
【解析】
(1)根据直角三角形的性质得到BD⊥AC,∠DBC=45°,根据角平分线的定义得到∠BAF=22.5°,根据三角形内角和定理计算,根据等腰三角形的判定定理证明即可;
(2)根据等腰三角形的概念解答.
(1)证明:∠ABC=90,BA=BC,点D为斜边AC的中点,
∴BD⊥AC,∠DBC=45°,
∵AF是∠BAC的平分线,
∴∠BAF=22.5°,
∴∠BFE=67.5°,
∴∠BEF=180°∠EBF∠EFB=67.5°,
∴∠BFE=∠BEF,
∴BE=BF;
(2)∵∠ABC=90°,BA=BC,点D为斜边AC的中点,
∴BD=AD=CD,
∴△ABD、△CBD是等腰三角形,
由已知得,△ABC是等腰三角形,
由(1)得,△BEF是等腰三角形,
∵AF是∠BAC的平分线,BD是∠ABC的平分线,
∴点E是△ABC的内心,
∴∠EAC=∠ECA=22.5°,
∴△AEC是等腰三角形.
∴△ABD、△CBD 、△ECA、△BEF是等腰三角形.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案科目:初中数学 来源: 题型:
【题目】某摩托车厂家本周计划每天生产300辆摩托车,由于工厂实行轮休,每天上班人数不一定相等,实际每天生产与计划相比情况如下表:
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | ﹣5 | +7 | ﹣3 | +4 | +10 | ﹣9 | ﹣25 |
(1)本周六生产了多少辆摩托车?
(2)本周总产量与计划相比是增加了还是减少了?具体数量是多少?产量最多的一天比产量最少的一天多生产了多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算与化简
(1)(﹣2x)3x6÷(﹣3x3)2
(2)5m(m﹣n)﹣(5m+n)(m﹣n)
(3)利用简便方法计算:20202﹣2019×2021
(4)先化简,再求值:[(a+b)2﹣(a﹣b)(a+b)]÷(2b),其中a=﹣![]() ,b=﹣1.
,b=﹣1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A、B两点在直线l的同一侧,线段AO,BM均是直线l的垂线段,且BM在AO的右边,AO=2BM,将BM沿直线l向右平移,在平移过程中,始终保持∠ABP=90°不变,BP边与直线l相交于点P.
(1)当P与O重合时(如图2所示),设点C是AO的中点,连接BC.求证:四边形OCBM是正方形;
(2)请利用如图1所示的情形,求证:![]() =
=![]() ;
;
(3)若AO=2![]() ,且当MO=2PO时,请直接写出AB和PB的长.
,且当MO=2PO时,请直接写出AB和PB的长.
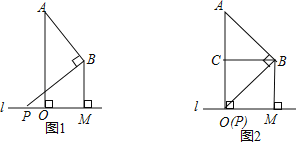
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是用4个全等的小长方形与1个小正方形密铺而成的正方形图案.已知该图案的面积为49,小正方形的面积为4,若分别用x,y(x >y)表示小长方形的长和宽,则下列关系式中不正确的是( )

A. x+y=7 B. x-y=2 C. x2 +y2=25 D. 4xy+4=49
查看答案和解析>>
科目:初中数学 来源: 题型:
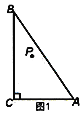
【题目】如图1.在△ABC中,∠ACB=90°,点P为△ABC内一点.
(1)连接PB、PC,将△BCP沿射线CA方向平移,得到△DAE,点B、C、P的对应点分别为点D、A、E,连接CE.
①依题意,请在图2中补全图形;
②如果BP⊥CE,AB+BP=9,CE=![]() ,求AB的长.
,求AB的长.
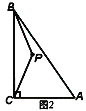
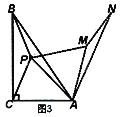
(2)如图3,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接PA、PB、PC,当AC=4,AB=8时,根据此图求PA+PB+PC的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
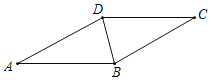
【题目】如图,BD是菱形ABCD的对角线,∠CBD=75°,
(1)请用尺规作图法,作AB的垂直平分线EF,垂足为E,交AD于F;(不要求写作法,保留作图痕迹)
(2)在(1)条件下,连接BF,求∠DBF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
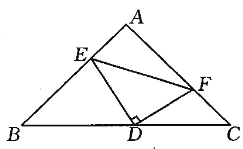
【题目】如图,在等腰直角△ABC中,AB=AC,点D是斜边BC的中点,点E、F分别是AB、AC边上的点,且DE⊥DF.
(1)证明:BE+CF=EF2;
(2)若BE=12,CF=5,求△DEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一个长方形的纸片制作一个无盖的长方体盒子,设这个长方形的长为a,宽为b,这个无盖的长方体盒子高为c,![]() 只考虑如图所示,在长方形的右边两个角上各剪去一个大小相同的正方形,左上角剪去一个长方形的情况
只考虑如图所示,在长方形的右边两个角上各剪去一个大小相同的正方形,左上角剪去一个长方形的情况![]() 若
若![]() ,则这个无盖长方体盒子的容积是______.
,则这个无盖长方体盒子的容积是______.
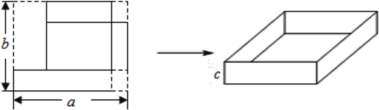
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com