
【题目】综合与探究
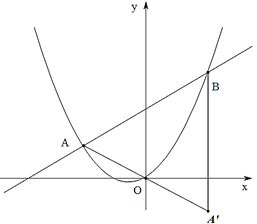
如图,抛物线![]() 的图象经过坐标原点O,且与
的图象经过坐标原点O,且与![]() 轴的另一交点为(
轴的另一交点为(![]() ,0).
,0).
(1)求抛物线的解析式;
(2)若直线![]() 与抛物线相交于点A和点B(点A在第二象限),设点A′是点A关于原点O的对称点,连接A′B,试判断ΔAA′B的形状,并说明理由;
与抛物线相交于点A和点B(点A在第二象限),设点A′是点A关于原点O的对称点,连接A′B,试判断ΔAA′B的形状,并说明理由;
(3)在问题(2)的基础上,探究:平面内是否存在点P,使得以点A,B,A′,P为顶点的四边形是菱形?若存在直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)ΔAA′B是等边三角形;(3)存在,
;(2)ΔAA′B是等边三角形;(3)存在,![]() ,
,![]() ,
,![]()
【解析】
(1)根据点的坐标,利用待定系数法即可求出抛物线F的解析式;
(2)先求出点A、B的坐标,利用对称性求出点A′的坐标,利用两点间的距离公式(勾股定理)可求出AB、AA′、A′B的值,由三者相等即可得出△AA′B为等边三角形;
(3)根据等边三角形的性质结合菱形的性质,可得出存在符合题意得点P,设点P的坐标为(x,y),分三种情况考虑:①当A′B为对角线时,根据菱形的性质(对角线互相平分)可求出点P的坐标;②当AB为对角线时,根据菱形的性质(对角线互相平分)可求出点P的坐标;③当AA′为对角线时,根据菱形的性质(对角线互相平分)可求出点P的坐标.综上即可得出结论.
解:(1)∵抛物线y=x2+bx+c的图象经过点(0,0)和(![]() ,0),
,0),
∴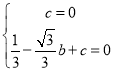 ,解得:
,解得: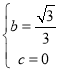 ;
;
∴![]() .
.
(2)ΔAA′B是等边三角形;
∵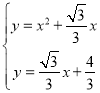 ,
,
解得: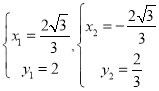 ,
,
∴A(![]() ),B(
),B(![]() ),
),
过点A分别作AC⊥![]() 轴,AD⊥A′B,垂足分别为C,D,
轴,AD⊥A′B,垂足分别为C,D,
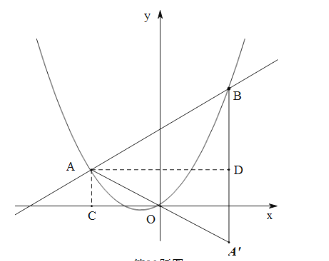
∴AC=![]() ,OC=
,OC=![]() ,
,
在RtΔAOC中
OA=![]() ,
,
∵点A′与点A关于原点对称,
∴A′(![]() ),AA′=
),AA′=![]() ,
,
∵B(![]() ),
),
∴A′B=2-(-![]() )=
)=![]() ,
,
又∵A(![]() ),B(
),B(![]() ),
),
∴AD=![]() ,BD=
,BD=![]() ,
,
在RtΔABD中
AB=![]() ,
,
∴AA′=A′B=AB,
∴ΔAA′B是等边三角形;
(3)存在符合题意的点P,且以点A、B、A′、P为顶点的菱形分三种情况;
设点P的坐标为:(x,y).
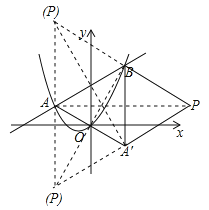
①当A′B为对角线时,有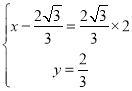 ,
,
解得: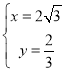 ,
,
∴点P为:![]() ;
;
②当AB为对角线时,有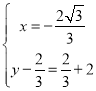 ,
,
解得: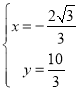 ,
,
∴点P为:![]() ;
;
③当AA′为对角线时,有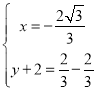 ,
,
解得: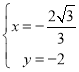 ,
,
∴点P为:![]() ;
;
综合上述,![]() ,
,![]() ,
,![]() .
.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
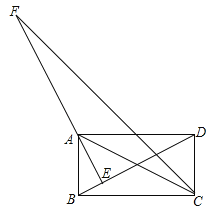
【题目】如图,矩形ABCD中,AE⊥BD于点E,CF平分∠BCD,交EA的延长线于点F,且BC=4,CD=2,给出下列结论:①∠BAE=∠CAD;②∠DBC=30°;③AE=![]() ;④AF=
;④AF=![]() ,其中正确结论的个数有( )
,其中正确结论的个数有( )
A.1个B.2个C.3个D.4个32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “明天降雨的概率是50%”表示明天有半天都在降雨
B. 数据4,3,5,5,0的中位数和众数都是5
C. 要了解一批钢化玻璃的最少允许碎片数,应采用普查的方式
D. 若甲、乙两组数中各有20个数据,平均数![]() =10,方差s2甲=1.25,s2乙=0.96,则说明乙组数据比甲组数据稳定
=10,方差s2甲=1.25,s2乙=0.96,则说明乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将图中的A型、B型、C型矩形纸片分别放在3个盒子中,盒子的形状、大小、质地都相同,再将这3个盒子装入一只不透明的袋子中.
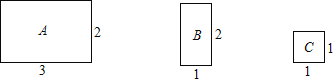
(1)搅匀后从中摸出1个盒子,求摸出的盒子中是![]() 型矩形纸片的概率;
型矩形纸片的概率;
(2)搅匀后先从中摸出1个盒子(不放回),再从余下的两个盒子中摸出一个盒子,求2次摸出的盒子的纸片能拼成一个新矩形的概率(不重叠无缝隙拼接).
查看答案和解析>>
科目:初中数学 来源: 题型:
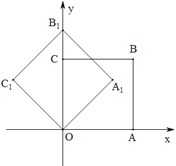
【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形![]() ,依此方式,绕点O连续旋转2018次得到正方形
,依此方式,绕点O连续旋转2018次得到正方形![]() ,如果点A的坐标为(1,0),那么点
,如果点A的坐标为(1,0),那么点![]() 的坐标是______.
的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、C的坐标分别为(0,8)、(6,0),以AC为直径作⊙O,交坐标轴于点B,点D是⊙O 上一点,且![]() ,过点D作DE⊥BC,垂足为E.
,过点D作DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)判断直线ED与⊙O的位置关系,并说明理由;
(3)求线段CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中的点P和图形M,给出如下的定义:若在图形M存在一点Q,使得P、Q两点间的距离小于或等于1,则称P为图形M的关联点.
中的点P和图形M,给出如下的定义:若在图形M存在一点Q,使得P、Q两点间的距离小于或等于1,则称P为图形M的关联点.
(1)当⊙O的半径为2时,
①在点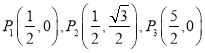 中,⊙O的关联点是_______________.
中,⊙O的关联点是_______________.
②点P在直线y=-x上,若P为⊙O 的关联点,求点P的横坐标的取值范围.
(2)⊙C 的圆心在x轴上,半径为2,直线y=-x+1与x轴、y轴交于点A、B.若线段AB上的所有点都是⊙C的关联点,直接写出圆心C的横坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=3,BC=4.以点C为圆心,r为半径的圆与边AB(边AB为线段)仅有一个公共点,则r的值为( )
A.r≥![]() B.r=3或r=4C.
B.r=3或r=4C.![]() ≤r≤4 D.r=
≤r≤4 D.r=![]() 或3<r≤4
或3<r≤4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com