【题目】在Rt△ABC中，∠ACB=90°，AC=3，BC=4．以点C为圆心，r为半径的圆与边AB（边AB为线段）仅有一个公共点，则r的值为（ ）
A.r≥
B.r=3或r=4C.≤r≤4 D.r=或3＜r≤4
科目：初中数学 来源： 题型：
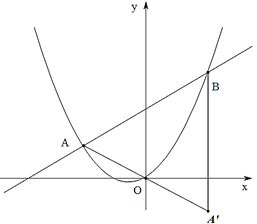
【题目】综合与探究
如图，抛物线
的图象经过坐标原点O，且与
轴的另一交点为(
，0).
(1)求抛物线的解析式；
(2)若直线
与抛物线相交于点A和点B(点A在第二象限)，设点A′是点A关于原点O的对称点，连接A′B，试判断ΔAA′B的形状，并说明理由；
(3)在问题(2)的基础上，探究：平面内是否存在点P，使得以点A，B，A′，P为顶点的四边形是菱形？若存在直接写出点P的坐标；若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
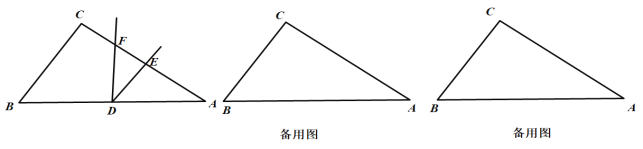
【题目】已知：如图，在
中，
，
，
，
是斜边
的中点，以为顶点，作
，
的两边交边
于点
、
（点不与点
重合）
（1）当
时，求
的长度；
（2）当绕点转动时，设
，
，求
关于
的函数解析式，并写出的取值范围.
（3）联结
，是否存在点，使△
与△
相似？若存在，请求出此时的长度；若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在甲、乙两名同学中选拔一人参加“英语口语听力”大赛，在相同的测试条件下，两人5次测试成绩（单位：分）如下：
甲：79，81，82，85，83 乙：88，79，90，81，72．
（1）求甲、乙两名同学测试成绩的方差；
（2）请你选择一个角度来判断选拔谁参加比赛更合适．
查看答案和解析>>
科目：初中数学 来源： 题型：
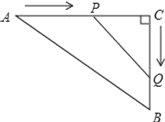
【题目】如图，在△ABC中，AB＝10
m，BC＝40m，∠C＝90°，点P从点A开始沿边AC边向点C以2m/s的速度匀速移动，同时另一点Q由C点开始以3m/s的速度沿着边CB匀速移动，几秒时，△PCQ的面积等于432m2？
查看答案和解析>>
科目：初中数学 来源： 题型：
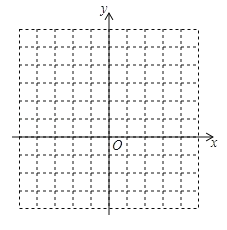
【题目】在平面直角坐标系中，抛物线y=ax2+bx+3经过点A（3，0）和点B（4，3）．
（1）求这条抛物线的函数表达式；
（2）求该抛物线的顶点坐标；
（3）在给定坐标系内画出这条抛物线．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】解方程：
（1）用开平方法解方程：
（2）用配方法解方程：x2 —4x+1=0
（3）用公式法解方程：3x2+5（2x+1）=0
（4）用因式分解法解方程：3（x-5）2=2（5-x）
（5）解方程：
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中的图形M，N，给出如下定义：P为图形M上任意一点，Q为图形N上任意一点，如果P，Q两点间的距离有最小值，那么称这个最小值为图形M，N间的“距离”，记作
特别地，若图形M，N有公共点，规定
．
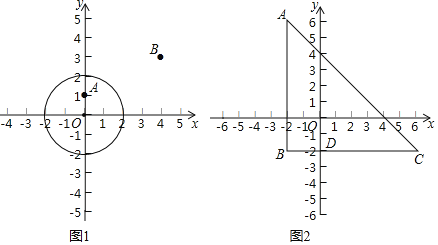
如图1，
的半径为2，
点
，
，则
______，
______．
已知直线l：
与的“距离”
，求b的值．
已知点
，
，
的圆心为
，半径为
若
，请直接写出m的取值范围______．
查看答案和解析>>
科目：初中数学 来源： 题型：
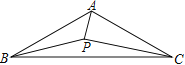
【题目】如图，△ABC中，AB＝AC，点P为△ABC内一点，∠APB＝∠BAC＝120°．若AP＋BP＝4，则PC的最小值为（ ）
A. 2B. 
C. 
D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
