练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

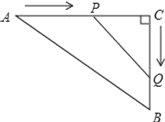
    【题目】如图，在△ABC中，AB＝10m，BC＝40m，∠C＝90°，点P从点A开始沿边AC边向点C以2m/s的速度匀速移动，同时另一点Q由C点开始以3m/s的速度沿着边CB匀速移动，几秒时，△PCQ的面积等于432m2？

    【答案】9秒时，△PCQ的面积等于432m2．

    【解析】

    根据勾股定理求出AC的长，然后根据运动速度，设x秒后，△PCQ的面积等于432m2，从而列出方程进一步求解即可。

    在△ABC中，AB＝10m，BC＝40m，∠C＝90°，

    ∴AC＝＝50m．

    设x秒时，△PCQ的面积等于432m2，

    依题意，得：×3x×（50﹣2x）＝432，

    解得：x1＝9，x2＝16．

    ∵3x＜40，

    ∴x＜13，

    ∴x＝9．

    答：9秒时，△PCQ的面积等于432m2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

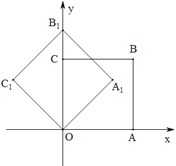
    【题目】如图，在平面直角坐标系中，将正方形OABC绕点O逆时针旋转45°后得到正方形,依此方式，绕点O连续旋转2018次得到正方形,如果点A的坐标为(1，0)，那么点的坐标是______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知圆0的直径AB垂直于弦CD于点E，CG是圆O的切线交AB的延长线于点G，连接CO并延长交AD于点F，且CFAD.

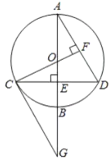
    （1）试问：CG//AD吗？说明理由：

    （2）证明：点E为OB的中点.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：如果一元二次方程满足，那么我们称这个方程为“凤凰”方程．已知是“凤凰”方程，且有两个相等的实数根，则下列结论正确的是 ( )

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝﹣1，与x轴的一个交点在（﹣3，0和（﹣2，0）之间，其部分图象如图，则下列结论：①2a﹣b＝0：②4ac﹣b2＜0：③点（x1，y1），（x2，y2）在抛物线上若x1＜x2，则y1＜y2；④a+b+c＜0．正确结论的个数是（　　）

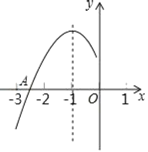
    A.1B.2C.3D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在Rt△ABC中，∠ACB=90°，AC=3，BC=4．以点C为圆心，r为半径的圆与边AB（边AB为线段）仅有一个公共点，则r的值为（　　）

    A.r≥B.r=3或r=4C.≤r≤4 D.r=或3＜r≤4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

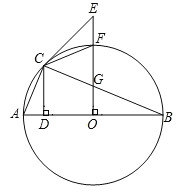
    【题目】如图，△ACB内接于圆O，AB为直径，CD⊥AB与点D，E为圆外一点，EO⊥AB，与BC交于点G，与圆O交于点F，连接EC，且EG=EC．

    （1）求证：EC是圆O的切线；

    （2）当∠ABC=22.5°时，连接CF．

    ①求证：AC=CF；

    ②若AD=1，求线段FG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某天猫店销售某种规格学生软式排球，成本为每个30元．以往销售大数据分析表明：当每只售价为40元时，平均每月售出600个；若售价每上涨1元，其月销售量就减少20个，若售价每下降1元，其月销售量就增加200个．

    （1）若售价上涨m元，每月能售出　　　个排球（用m的代数式表示）．

    （2）为迎接“双十一”，该天猫店在10月底备货1300个该规格的排球，并决定整个11月份进行降价促销，问售价定为多少元时，能使11月份这种规格排球获利恰好为8400元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示,在平面直角坐标系中,把矩形OCBA绕点C顺时针旋转α角,得到矩形FCDE,设FC与AB交于点H,且A(0,4),C(6,0).

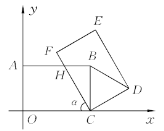
    (1)当α=45°时，求H点的坐标.

    (2)当α=60°时,ΔCBD是什么特殊的三角形?说明理由.

    (3)当AH=HC时,求直线HC的解析式.

    查看答案和解析>>

    同步练习册答案