
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点在(﹣3,0和(﹣2,0)之间,其部分图象如图,则下列结论:①2a﹣b=0:②4ac﹣b2<0:③点(x1,y1),(x2,y2)在抛物线上若x1<x2,则y1<y2;④a+b+c<0.正确结论的个数是( )
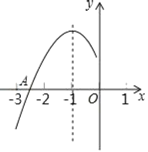
A.1B.2C.3D.4
科目:初中数学 来源: 题型:
【题目】如图,把正方形ABCD绕点C按顺时针方向旋转![]() 得到正方形
得到正方形![]() 此时,点
此时,点![]() 落在对角线AC上,点
落在对角线AC上,点![]() 落在CD的延长线上
落在CD的延长线上![]() ,
,![]() 交AD于点E,连接
交AD于点E,连接![]() 、CE.
、CE.
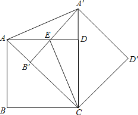
求证:(1)![]() ≌
≌![]() ;
;
(2)直线CE是线段![]() 的垂直平分线.
的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的顶点为D(﹣1,3),与x轴的一个交点在(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:
①b2+4ac>0;②c﹣a=3;③a+b+c<0;④方程ax2+bx+c=m(m≥2)一定有实数根,其中正确的结论为( )
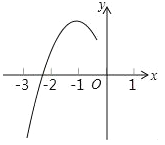
A.②③ B.①③ C.①②③ D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=3,点P是边AB上的一动点,连结DP.
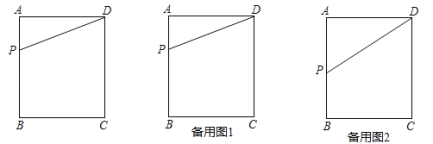
(1)若将△DAP沿DP折叠,点A落在矩形的对角线上点A′处,试求AP的长;
(2)点P运动到某一时刻,过点P作直线PE交BC于点E,将△DAP与△PBE分别沿DP与PE折叠,点A与点B分别落在点A′,B′处,若P,A′,B′三点恰好在同一直线上,且A′B′=2,试求此时AP的长;
(3)当点P运动到边AB的中点处时,过点P作直线PG交BC于点G,将△DAP与△PBG分别沿DP与PG折叠,点A与点B重合于点F处,连结CF,请求出CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA
与⊙O的另一个交点为E,连结AC,CE。

(1)求证:∠B=∠D;
(2)若AB=4,BC-AC=2,求CE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
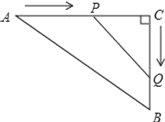
【题目】如图,在△ABC中,AB=10![]() m,BC=40m,∠C=90°,点P从点A开始沿边AC边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着边CB匀速移动,几秒时,△PCQ的面积等于432m2?
m,BC=40m,∠C=90°,点P从点A开始沿边AC边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着边CB匀速移动,几秒时,△PCQ的面积等于432m2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成下面的统计图.
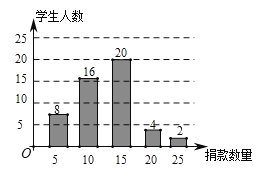
(1)这50名同学捐款的众数为 元,中位数为 元;
(2)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
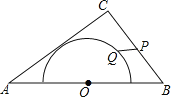
【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最大值与最小值的和是__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com