
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌABЃН4ЃЌBCЃН3ЃЌЕуPЪЧБпABЩЯЕФвЛЖЏЕуЃЌСЌНсDPЃЎ
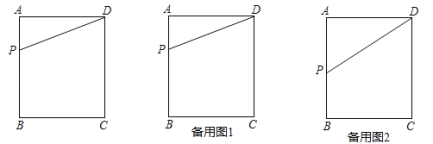
ЃЈ1ЃЉШєНЋЁїDAPбиDPелЕўЃЌЕуAТфдкОиаЮЕФЖдНЧЯпЩЯЕуAЁфДІЃЌЪдЧѓAPЕФГЄЃЛ
ЃЈ2ЃЉЕуPдЫЖЏЕНФГвЛЪБПЬЃЌЙ§ЕуPзїжБЯпPEНЛBCгкЕуEЃЌНЋЁїDAPгыЁїPBEЗжБ№биDPгыPEелЕўЃЌЕуAгыЕуBЗжБ№ТфдкЕуAЁфЃЌBЁфДІЃЌШєPЃЌAЁфЃЌBЁфШ§ЕуЧЁКУдкЭЌвЛжБЯпЩЯЃЌЧвAЁфBЁфЃН2ЃЌЪдЧѓДЫЪБAPЕФГЄЃЛ
ЃЈ3ЃЉЕБЕуPдЫЖЏЕНБпABЕФжаЕуДІЪБЃЌЙ§ЕуPзїжБЯпPGНЛBCгкЕуGЃЌНЋЁїDAPгыЁїPBGЗжБ№биDPгыPGелЕўЃЌЕуAгыЕуBжиКЯгкЕуFДІЃЌСЌНсCFЃЌЧыЧѓГіCFЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉAPЕФГЄЮЊ![]() Лђ
Лђ![]() ЃЛЃЈ2ЃЉPAЕФГЄЮЊ1Лђ3ЃЛЃЈ3ЃЉCFЃН
ЃЛЃЈ2ЃЉPAЕФГЄЮЊ1Лђ3ЃЛЃЈ3ЃЉCFЃН![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЗжСНжжЧщаЮЃКЂйЕБЕуAТфдкЖдНЧЯпBDЩЯЪБЃЌЩшAP=PAЁф=xЃЌЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЛЂкЕБЕуAТфдкЖдНЧЯпACЩЯЪБЃЌРћгУЯрЫЦШ§НЧаЮЕФаджЪЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉЗжСНжжЧщаЮЗжБ№ЧѓНтМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉШчЭМ5жаЃЌзїFHЁЭCDгЩHЃЎЯыАьЗЈЧѓГіFHЁЂCHМДПЩНтОіЮЪЬтЃЛ
ЃЈ1ЃЉЂйЕБЕуAТфдкЖдНЧЯпBDЩЯЪБЃЌЩшAPЃНPAЁфЃНxЃЌ
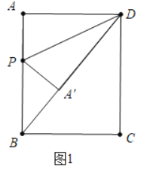
дкRtЁїADBжаЃЌЁпABЃН4ЃЌADЃН3ЃЌЁрBDЃН![]() ЃН5ЃЌ
ЃН5ЃЌ
ЁпABЃНDAЁфЃН3ЃЌЁрBAЁфЃН2ЃЌ
дкRtЁїBPAЁфжаЃЌЃЈ4ЉxЃЉ2ЃНx2+22ЃЌНтЕУxЃН![]() ЃЌ
ЃЌ
ЁрAPЃН![]() ЃЎ
ЃЎ
ЂкЕБЕуAТфдкЖдНЧЯпACЩЯЪБЃЌ
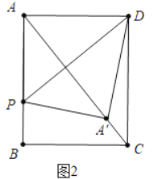
гЩЗеладжЪПЩжЊЃКPDЁЭACЃЌдђгаЁїDAPЁзЁїABCЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌЁрAPЃН
ЃЌЁрAPЃН![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЎ
ЃЎ
ЁрAPЕФГЄЮЊ![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйШчЭМ3жаЃЌЩшAPЃНxЃЌдђPBЃН4ЉxЃЌ
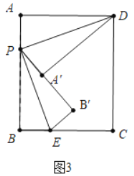
ИљОнелЕўЕФаджЪПЩжЊЃКPAЃНPAЁфЃНxЃЌPBЃНPBЁфЃН4ЉxЃЌ
ЁпAЁфBЁфЃН2ЃЌЁр4ЉxЉxЃН2ЃЌЁрxЃН1ЃЌЁрPAЃН1ЃЛ
ЂкШчЭМ4жаЃЌ

ЩшAPЃНxЃЌдђPBЃН4ЉxЃЌ
ИљОнелЕўЕФаджЪПЩжЊЃКPAЃНPAЁфЃНxЃЌPBЃНPBЁфЃН4ЉxЃЌ
ЁпAЁфBЁфЃН2ЃЌЁрxЉЃЈ4ЉxЃЉЃН2ЃЌ
ЁрxЃН3ЃЌЁрPAЃН3ЃЛ
злЩЯЫљЪіЃЌPAЕФГЄЮЊ1Лђ3ЃЛ
ЃЈ3ЃЉШчЭМ5жаЃЌзїFHЁЭCDгЩHЃЎ
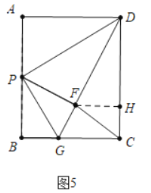
гЩЗелЕФаджЪПЩжЊЃЛADЃНDFЃН3ЃЎBGЃНBFЃЌGЁЂFЁЂDЙВЯпЃЌ
ЩшBGЃНFGЃНxЃЌдкRtЁїGCDжаЃЌЃЈx+3ЃЉ2ЃН42+ЃЈ3ЉxЃЉ2ЃЌ
НтЕУxЃН![]() ЃЌЁрDGЃНDF+FGЃН
ЃЌЁрDGЃНDF+FGЃН![]() ЃЌCGЃНBCЉBGЃН
ЃЌCGЃНBCЉBGЃН![]() ЃЌ
ЃЌ
ЁпFHЁЮCGЃЌЁр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌЁр
ЃЌЁр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрFHЃН![]() ЃЌDHЃН
ЃЌDHЃН![]() ЃЌЁрCHЃН4Љ
ЃЌЁрCHЃН4Љ![]() ЃН
ЃН![]() ЃЌ
ЃЌ
дкRtЁїCFHжаЃЌCFЃН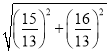 ЃН
ЃН![]() ЃЎ
ЃЎ


 ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИ
ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИ злКЯздВтЯЕСаД№АИ
злКЯздВтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯп![]() ЕФЖЅЕуЮЊ
ЕФЖЅЕуЮЊ![]() ЃЌгы
ЃЌгы![]() жсЯрНЛгкЕу
жсЯрНЛгкЕу![]() ЃЌЖдГЦжсЮЊжБЯп
ЃЌЖдГЦжсЮЊжБЯп![]() ЃЌЕу
ЃЌЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЕФжаЕу.
ЕФжаЕу.
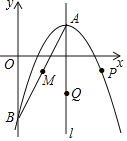
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉаДГіЕу![]() ЕФзјБъВЂЧѓжБЯп
ЕФзјБъВЂЧѓжБЯп![]() ЕФБэДяЪНЃЛ
ЕФБэДяЪНЃЛ
ЃЈ3ЃЉЩшЖЏЕу![]() ЃЌ
ЃЌ![]() ЗжБ№дкХзЮяЯпКЭЖдГЦжсlЩЯЃЌЕБвд
ЗжБ№дкХзЮяЯпКЭЖдГЦжсlЩЯЃЌЕБвд![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЪБЃЌЧѓ
ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЪБЃЌЧѓ![]() ЃЌ
ЃЌ![]() СНЕуЕФзјБъ.
СНЕуЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃК
Ъ§бЇЛюЖЏПЮЩЯЃЌРюРЯЪІИјГіШчЯТЖЈвхЃКШчЙћвЛИіШ§НЧаЮгавЛБпЩЯЕФжаЯпЕШгкетЬѕБпЕФвЛАыЃЌФЧУДГЦШ§НЧаЮЮЊЁАжЧЛлШ§НЧаЮЁБ.

РэНтЃК
ЂХШчЭМ![]() ЃЌвбжЊ
ЃЌвбжЊ![]() ЪЧЁб
ЪЧЁб![]() ЩЯСНЕуЃЌЧыдкдВЩЯевГіТњзуЬѕМўЕФЕу
ЩЯСНЕуЃЌЧыдкдВЩЯевГіТњзуЬѕМўЕФЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЮЊЁАжЧЛлШ§НЧаЮЁБЃЈЛГіЕу
ЮЊЁАжЧЛлШ§НЧаЮЁБЃЈЛГіЕу![]() ЕФЮЛжУЃЌБЃСєзїЭМКлМЃЃЉЃЛ
ЕФЮЛжУЃЌБЃСєзїЭМКлМЃЃЉЃЛ
ЂЦШчЭМ![]() ЃЌдке§ЗНаЮ
ЃЌдке§ЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЪЧ
ЪЧ![]() ЩЯвЛЕуЃЌЧв
ЩЯвЛЕуЃЌЧв![]() ЃЌЪдХаЖЯ
ЃЌЪдХаЖЯ![]() ЪЧЗёЮЊЁАжЧЛлШ§НЧаЮЁБЃЌВЂЫЕУїРэгЩЃЛ
ЪЧЗёЮЊЁАжЧЛлШ§НЧаЮЁБЃЌВЂЫЕУїРэгЩЃЛ
дЫгУЃК
ЂЧШчЭМ![]() ЃЌдкЦНУцжБНЧзјБъЯЕ
ЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЁб
жаЃЌЁб![]() ЕФАыОЖЮЊ
ЕФАыОЖЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯЕФвЛЕуЃЌШєдкЁб
ЩЯЕФвЛЕуЃЌШєдкЁб![]() ЩЯДцдквЛЕу
ЩЯДцдквЛЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЮЊЁАжЧЛлШ§НЧаЮЁБЃЌЕБЦфУцЛ§ШЁЕУзюаЁжЕЪБЃЌжБНгаДГіДЫЪБЕу
ЮЊЁАжЧЛлШ§НЧаЮЁБЃЌЕБЦфУцЛ§ШЁЕУзюаЁжЕЪБЃЌжБНгаДГіДЫЪБЕу![]() ЕФзјБъ.
ЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдВ0ЕФжБОЖABДЙжБгкЯвCDгкЕуEЃЌCGЪЧдВOЕФЧаЯпНЛABЕФбгГЄЯпгкЕуGЃЌСЌНгCOВЂбгГЄНЛADгкЕуFЃЌЧвCF![]() AD.
AD.
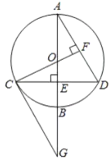
ЃЈ1ЃЉЪдЮЪЃКCG//ADТ№ЃПЫЕУїРэгЩЃК
ЃЈ2ЃЉжЄУїЃКЕуEЮЊOBЕФжаЕу.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкНтОіЪ§бЇЮЪЬтЪБЃЌЮвУЧГЃГЃДгЬиЪтШыЪжЃЌВТЯыНсТлЃЌВЂГЂЪдЗЂЯжНтОіЮЪЬтЕФВпТдгыЗНЗЈЃЎ
ЃЈЮЪЬтЬсГіЃЉ
ЧѓжЄЃКШчЙћвЛИіЖЈдВЕФФкНгЫФБпаЮЖдНЧЯпЛЅЯрДЙжБЃЌФЧУДетИіЫФБпаЮЕФЖдБпЕФЦНЗНКЭЪЧвЛИіЖЈжЕЃЎ
ЃЈДгЬиЪтШыЪжЃЉ
ЮвУЧВЛЗСЩшЖЈдВOЕФАыОЖЪЧRЃЌЁбOЕФФкНгЫФБпаЮABCDжаЃЌACЁЭBDЃЎ
ЧыФудкЭМЂйжаВЙШЋЬиЪтЪтЮЛжУЪБЕФЭМаЮЃЌВЂНшжњгкЫљЛЭМаЮЬНОПЮЪЬтЕФНсТлЃЎ

ЃЈЮЪЬтНтОіЃЉ
вбжЊЃКШчЭМЂкЃЌЖЈдВЁбOЕФАыОЖЪЧRЃЌЫФБпаЮABCDЪЧЁбOЕФФкНгЫФБпаЮЃЌ ACЁЭBDЃЎ
ЧѓжЄЃК ЃЎ
жЄУїЃК

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКШчЙћвЛдЊЖўДЮЗНГЬ![]() Тњзу
Тњзу![]() ЃЌФЧУДЮвУЧГЦетИіЗНГЬЮЊЁАЗяЛЫЁБЗНГЬЃЎвбжЊ
ЃЌФЧУДЮвУЧГЦетИіЗНГЬЮЊЁАЗяЛЫЁБЗНГЬЃЎвбжЊ![]() ЪЧЁАЗяЛЫЁБЗНГЬЃЌЧвгаСНИіЯрЕШЕФЪЕЪ§ИљЃЌдђЯТСаНсТле§ШЗЕФЪЧ ( )
ЪЧЁАЗяЛЫЁБЗНГЬЃЌЧвгаСНИіЯрЕШЕФЪЕЪ§ИљЃЌдђЯТСаНсТле§ШЗЕФЪЧ ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯпyЃНax2+bx+cЃЈaЁй0ЃЉЕФЖдГЦжсЮЊжБЯпxЃНЉ1ЃЌгыxжсЕФвЛИіНЛЕудкЃЈЉ3ЃЌ0КЭЃЈЉ2ЃЌ0ЃЉжЎМфЃЌЦфВПЗжЭМЯѓШчЭМЃЌдђЯТСаНсТлЃКЂй2aЉbЃН0ЃКЂк4acЉb2ЃМ0ЃКЂлЕуЃЈx1ЃЌy1ЃЉЃЌЃЈx2ЃЌy2ЃЉдкХзЮяЯпЩЯШєx1ЃМx2ЃЌдђy1ЃМy2ЃЛЂмa+b+cЃМ0ЃЎе§ШЗНсТлЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
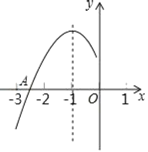
A.1B.2C.3D.4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
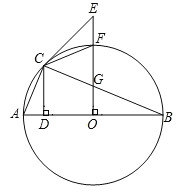
ЁОЬтФПЁПШчЭМЃЌЁїACBФкНггкдВOЃЌABЮЊжБОЖЃЌCDЁЭABгыЕуDЃЌEЮЊдВЭтвЛЕуЃЌEOЁЭABЃЌгыBCНЛгкЕуGЃЌгыдВOНЛгкЕуFЃЌСЌНгECЃЌЧвEG=ECЃЎ
ЃЈ1ЃЉЧѓжЄЃКECЪЧдВOЕФЧаЯпЃЛ
ЃЈ2ЃЉЕБЁЯABC=22.5ЁуЪБЃЌСЌНгCFЃЎ
ЂйЧѓжЄЃКAC=CFЃЛ
ЂкШєAD=1ЃЌЧѓЯпЖЮFGЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНax2ЃЋbxЃЋcЕФЭМЯѓШчЭМЫљЪОЃЌгавдЯТНсТлЃКЂйabcЃО0ЃЛЂкaЃbЃЋcЃМ0ЃЛЂл2aЃНbЃЛЂм4aЃЋ2bЃЋcЃО0ЃЛЂнШєЕу(Ѓ2ЃЌy1)КЭ(Ѓ![]() ЃЌy2)дкИУЭМЯѓЩЯЃЌдђy1ЃОy2. Цфжае§ШЗЕФНсТлИіЪ§ЪЧ ( )
ЃЌy2)дкИУЭМЯѓЩЯЃЌдђy1ЃОy2. Цфжае§ШЗЕФНсТлИіЪ§ЪЧ ( )
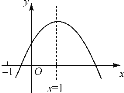
A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com