
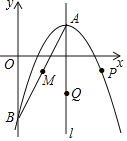
【题目】如图,已知抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,对称轴为直线
,对称轴为直线![]() ,点
,点![]() 是线段
是线段![]() 的中点.
的中点.
(1)求抛物线的表达式;
(2)写出点![]() 的坐标并求直线
的坐标并求直线![]() 的表达式;
的表达式;
(3)设动点![]() ,
,![]() 分别在抛物线和对称轴l上,当以
分别在抛物线和对称轴l上,当以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形时,求
为顶点的四边形是平行四边形时,求![]() ,
,![]() 两点的坐标.
两点的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)点
;(3)点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 或
或![]() 、
、![]() 或
或![]() .
.
【解析】
(1)函数表达式为:![]() ,将点
,将点![]() 坐标代入上式,即可求解;
坐标代入上式,即可求解;
(2)![]() 、
、![]() ,则点
,则点![]() ,设直线
,设直线![]() 的表达式为:
的表达式为:![]() ,将点
,将点![]() 坐标代入上式,即可求解;
坐标代入上式,即可求解;
(3)分当![]() 是平行四边形的一条边、
是平行四边形的一条边、![]() 是平行四边形的对角线两种情况,分别求解即可.
是平行四边形的对角线两种情况,分别求解即可.
解:(1)函数表达式为:![]() ,
,
将点![]() 坐标代入上式并解得:
坐标代入上式并解得:![]() ,
,
故抛物线的表达式为:![]() ;
;
(2)![]() 、
、![]() ,则点
,则点![]() ,
,
设直线![]() 的表达式为:
的表达式为:![]() ,
,
将点![]() 坐标代入上式得:
坐标代入上式得:![]() ,解得:
,解得:![]() ,
,
故直线![]() 的表达式为:
的表达式为:![]() ;
;
(3)设点![]() 、点
、点![]() ,
,
①当![]() 是平行四边形的一条边时,
是平行四边形的一条边时,
点![]() 向左平移2个单位、向下平移4个单位得到
向左平移2个单位、向下平移4个单位得到![]() ,
,
同样点![]() 向左平移2个单位、向下平移4个单位得到
向左平移2个单位、向下平移4个单位得到![]() ,
,
即:![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,
故点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ;
;
②当![]() 是平行四边形的对角线时,
是平行四边形的对角线时,
由中点定理得:![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,
故点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ;
;
故点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() ,
,![]() 或
或![]() 、
、![]() ,
,![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】有形状、大小和质地都相同的四张卡片,正面分别写有A,B,C,D和一个等式,将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.
![]()
(1)用画树状图或列表的方法表示抽取两张卡片可能出现的所有情况(结果用A,B,C,D表示).
(2)小明和小强按下面规则做游戏:抽取的两张卡片上若等式都不成立,则小明胜;若至少有一个等式成立,则小强胜.你认为这个游戏公平吗?若公平,请说明理由;若不公平,则这个规则对谁有利?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(0,2),B(p,q)在直线上,抛物线m经过点B、C(p+4,q),且它的顶点N在直线l上.
(1)若B(-2,1),
①请在平面直角坐标系中画出直线l与抛物线m的示意图;
②设抛物线m上的点Q的模坐标为e(-2≤e≤0)过点Q作x轴的垂线,与直线l交于点H.若QH=d,当d随e的增大面增大时,求e的取值范围;
(2)抛物线m与y轴交于点F,当抛物线m与x轴有唯一交点时,判断△NOF的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
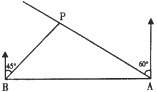
【题目】如图,在一笔直的海岸线上有A,B两个观测站,A在B的正东方向,有一艘小船停在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,BP=6![]() km.
km.
(1)求A、B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向前行,求观测站B与小船的最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
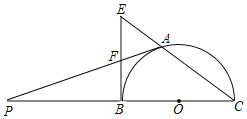
【题目】如图,BC是半⊙O的直径,A是⊙O上一点,过点的切线交CB的延长线于点P,过点B的切线交CA的延长线于点E,AP与BE相交于点F.
(1)求证:BF=EF;
(2)若AF=![]() ,半⊙O的半径为2,求PA的长度.
,半⊙O的半径为2,求PA的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC为⊙O的直径,以BC为直角边作Rt△ABC,∠ACB=90°,斜边AB与⊙O交于点D,过点D作⊙O的切线DE交AC于点E,DG⊥BC于点F,交⊙O于点G.

(1)求证:AE=CE;
(2)若AD=4,AE=![]() ,求DG的长.
,求DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC与△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,AC=BC=4,AD=DE,点F是BE的中点,连接DF,CF.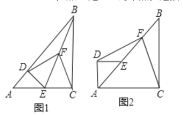
(1)如图1,当点D在AB上,且点E是AC的中点时,求CF的长.
(2)如图1,若点D落在AB上,点E落在AC上,证明:DF⊥CF.
(3)如图2,当AD⊥AC,且E点落在AC上时,判断DF与CF之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
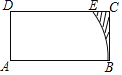
【题目】如图,矩形ABCD中,AB=2AD,以A为圆心,AB长为半径作弧BE,CD于E,若AB=4,则阴影部分的面积为_____(结果保留π和根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求抛物线的解析式和直线AC的解析式;
(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;
(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com