
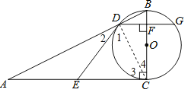
【题目】如图,BC为⊙O的直径,以BC为直角边作Rt△ABC,∠ACB=90°,斜边AB与⊙O交于点D,过点D作⊙O的切线DE交AC于点E,DG⊥BC于点F,交⊙O于点G.

(1)求证:AE=CE;
(2)若AD=4,AE=![]() ,求DG的长.
,求DG的长.
【答案】(1)证明见解析 ;(2)![]()
【解析】
(1)首先连接CD,由BC为⊙O的直径,∠ACB=90°,可得AC是⊙O的切线.又由⊙O的切线DE交AC于点E,根据切线长定理,可得ED=EC,然后由等角的余角相等,证得∠A=∠2,即可得:AE=CE;
(2)首先由直角三角形斜边上的中线等于斜边的一半,求得AC长,然后由勾股定理,求得CD的长,再利用三角函数,求得DG的长.
解:(1)如图,连接CD,
∵BC为⊙O的直径,∠ACB=90°,
∴AC是⊙O的切线,
又∵DE与⊙O相切,
∴ED=EC,
∴∠1=∠3,
∵BC为⊙O的直径,
∴∠BDC=90°,
∵∠1+∠2=∠3+∠A=90°,
∴∠A=∠2,
∴ED=EA,
∴AE=CE;
(2)∵AE=![]() ,
,
∴AC=2AE=![]() . 在Rt△ACD中,
. 在Rt△ACD中,![]() ,
,
![]() ,
,
∵∠3+∠4=∠3+∠A=90°,
∴∠A=∠4,
![]() ,
,
![]() ,
,
∵DG⊥BC于点F,
∴DG=2DF=![]() .
.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,过点C的切线交AB的延长线于点D,∠ACD=120°.
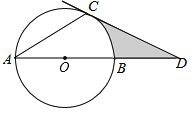
(1)求证:AC=CD;
(2)若⊙O的半径为2,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=﹣x2﹣4x+5交x轴于点A、B两点(点A在点B的左侧),交y轴于点C,点D为抛物线的顶点,连接AD.
(1)求直线AD的解析式.
(2)点E(m,0)、F(m+1,0)为x轴上两点,其中(﹣5<m<﹣3.5)EE′、FF′分别平行于y轴,交抛物线于点E′和F′,交AD于点M、N,当ME′+NF′的值最大时,在y轴上找一点R,使得|RE′﹣RF′|值最大,请求出点R的坐标及|RE′﹣RF′|的最大值.
(3)如图2,在抛物线上是否存在点P,使得△PAC是以AC为底边的等腰三角形,若存在,请出点P的坐标及△PAC的面积,若不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
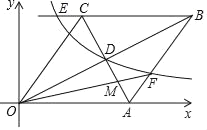
【题目】如图,菱形OABC,A点的坐标为(5,0),对角线OB、AC相交于D点,双曲线y=![]() (x>0)经过D点,交BC的延长线于E点,交AB于F点,连接OF交AC于M,且OBAC=40.有下列四个结论:①k=8;②CE=1;③AC+OB=6
(x>0)经过D点,交BC的延长线于E点,交AB于F点,连接OF交AC于M,且OBAC=40.有下列四个结论:①k=8;②CE=1;③AC+OB=6![]() ;④S△AFM:S△AOM=1:3.其中正确的结论是( )
;④S△AFM:S△AOM=1:3.其中正确的结论是( )
A. ①②B. ①③C. ①②③D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
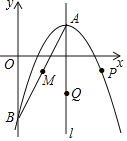
【题目】如图,已知抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,对称轴为直线
,对称轴为直线![]() ,点
,点![]() 是线段
是线段![]() 的中点.
的中点.
(1)求抛物线的表达式;
(2)写出点![]() 的坐标并求直线
的坐标并求直线![]() 的表达式;
的表达式;
(3)设动点![]() ,
,![]() 分别在抛物线和对称轴l上,当以
分别在抛物线和对称轴l上,当以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形时,求
为顶点的四边形是平行四边形时,求![]() ,
,![]() 两点的坐标.
两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
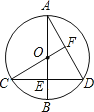
【题目】如图,已知⊙O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD
(1) 求证:E是OB的中点
(2) 若AB=8,求CD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
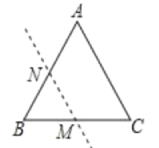
【题目】(1)(探究)如图,在等边△ABC中,AB=4cm,点M为边BC的中点,点N为边AB上的任意一点(不与点A,B重合).若点B关于直线MN的对称点B′恰好落在等边△ABC的边上,求BN的长.
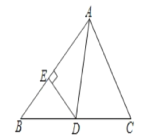
(2)(拓展)如图,在△ABC中,∠ABC=45°,AD是BC边上的中线,过点D作DE⊥AB于点E,且sin∠DAB=![]() ,DB=3
,DB=3![]() .求AB的长.
.求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆小面是一款发源于山城重庆的地方特色传统小吃,是重庆最受欢迎的美食之一.重庆小面佐料丰富且用料考究,不同店面还根据自身菜谱加入豌豆、牛肉、肥肠、杂酱等,口感独特,麻辣鲜香,近年来闻名全国,某天,小明家花了48元购买牛肉面作为早饭,小华家花了28元购买豌豆面作为早饭,且小明家购买牛肉面的碗数与小华家购买豌豆面的碗数相同.已知面馆一碗豌豆面的价格比一碗牛肉面的价格少5元.
(1)求购买一碗豌豆面和一碗牛肉面各需要多少元?
(2)面馆一碗豌豆面的成本为4元,一碗牛肉面的成本为7元,某天面馆卖出豌豆面和牛肉面共400碗,且卖出的豌豆面和牛肉面的总利润不低于1800元,则面馆当天至少卖出牛肉面多少碗?
查看答案和解析>>
科目:初中数学 来源: 题型:
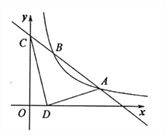
【题目】如图,已知一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点
的图像交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求反比例函数和一次函数的表达式.
(2)若在![]() 轴上有一点
轴上有一点![]() ,其横坐标是1,连接
,其横坐标是1,连接![]() 、
、![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com