
����Ŀ����ͼ1����֪������y=��x2��4x+5��x���ڵ�A��B���㣨��A�ڵ�B����ࣩ����y���ڵ�C����DΪ�����ߵĶ��㣬����AD��
��1����ֱ��AD�Ľ���ʽ��
��2����E��m��0����F��m+1��0��Ϊx�������㣬���У���5��m����3.5��EE�䡢FF���ֱ�ƽ����y�ᣬ���������ڵ�E����F������AD�ڵ�M��N����ME��+NF����ֵ���ʱ����y������һ��R��ʹ��|RE�䩁RF��|ֵ����������R�����꼰|RE�䩁RF��|�����ֵ��
��3����ͼ2�������������Ƿ���ڵ�P��ʹ����PAC����ACΪ�ױߵĵ��������Σ������ڣ������P�����꼰��PAC��������������ڣ���˵��������

���𰸡���1��y=3x+15����2����R�������ǣ�0��17�������ֵΪ![]() ����3�����ڣ�P��
����3�����ڣ�P��![]() ����P�䣨
����P�䣨![]() �������Ϊ
�������Ϊ![]()
��������
(1)���������ߵĽ���ʽ��õ�A��D�����꣬Ȼ�����ô���ϵ��������ֱ��AD�Ľ���ʽ����;
(2)����ƽ���ߵ����ʺͺ���ͼ���ϵ������������
ME'�� NF'����m2��7m��10��m2��9m��18��2m2��16m��28;��϶��κ�����ֵ����������߶���̵õ�:Ҫʹ|RE���� RF��|ֵ������E'��F����R������һ��ֱ����,ֻ����õ�E'��F'�����꣬���ô���ϵ������ֱ֪��E'F'��ϵʽ���ɸù�ϵʽ�����R�����꼴��;
(3)��PA �� PCʱ,��P���߶�AC�Ĵ�ֱƽ������,��������ε������ʽ���н��.
��1����ͼ1����y=��x2��4x+5=����x+5����x��1����y=����x+2��2+9��
��A����5��0����B��1��0����D����2��9����
��ֱ��AD�Ľ���ʽΪ��y=kx+b��k��0������A��D��������룬��
![]() ��
��
���![]() ��
��
��ֱ��AD�Ľ���ʽΪ��y=3x+15��
��2����ͼ1����EE����y�ᣬFF����y�ᣬE��m��0����F��m+1��0����
��E��m����m2��4m+5����F��m+1������m+1��2��4��m+1��+5����M��m��3m+15����N��m+1��3��m+1��+15����
��ME��=��m2��4m+5����3m+15��=��m2��7m��10��NF��=��m2��9m��18��
��ME��+NF��=��m2��7m��10��m2��9m��18=2m2��16m��28��
����2��0��
��m=��![]() =��4��
=��4��
��ME��+NF�������ֵ����ʱE�䣨��4��5����F�䣨��3��8����
 Ҫʹ|RE�䩁RF��|ֵ������E�䡢F�䡢R������һ��ֱ���ϣ�
Ҫʹ|RE�䩁RF��|ֵ������E�䡢F�䡢R������һ��ֱ���ϣ�
����ֱ��E��F�䣺y=kx+b��k��0������
![]() ��
��
���![]() ��
��
��ֱ��E��F�䣺y=3x+17��k��0����
��x=0ʱ��y=17�����R�������ǣ�0��17����
��ʱ��|RE�䩁RF��|�����ֵΪ![]() =
=![]() ��
��
��3����ͼ2�����P��x����x2��4x+5����
��PA=PCʱ����P���߶�AC�Ĵ�ֱƽ�����ϣ�
��OC=OA��
���O���߶�AC�Ĵ�ֱƽ�����ϣ�
���P�ڡ�AOC�Ľ�ƽ�����ϣ�
����x=��x2��4x+5��
���x1=![]() ��x2=
��x2=![]() ��
��
��P��![]() ��
��![]() ����P�䣨
����P�䣨![]() ��
��![]() ����
����
��PH=OP��OH=![]() ��P��H=OP��+OH=
��P��H=OP��+OH=![]() ��
��
��S��PAC=![]() ACPH=
ACPH=![]() ��5
��5![]() ��
��![]() =
=![]() ��S��PAC=
��S��PAC=![]() ACP��H=
ACP��H=![]() ��5
��5![]() ��
��![]() =
=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
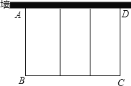
����Ŀ����ͼ��Ҫ����һ��ǽ(ǽ��Ϊ25��)����Ȧ����100��Χ��Χ��������С��ͬ�ľ�����Ȧ.
(1)����Ȧ�����Ϊ400ƽ���ף�����Ȧ�ı߳�AB, BC��Ϊ������?
(2) ������Ȧ�Ļ����ṹ������Ȧ������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڰ뾶Ϊ2������AOB�У���AOB=90�㣬��C�ǻ� AB�ϵ�һ�����㣨�����A��B�غϣ�OD��BC��OE��AC������ֱ�Ϊ��D��E���ڵ�C���˶������У�����˵����ȷ���ǣ� ��
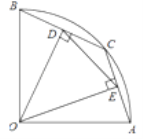
A. ����AOB�����Ϊ![]() B. ��BC�ij�Ϊ
B. ��BC�ij�Ϊ![]() C. ��DOE=45�� D. �߶�DE�ij���
C. ��DOE=45�� D. �߶�DE�ij���![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����OΪ��ABC�����Բ��BCΪֱ������E��AB�ϣ�����E��EF��BC����G��FE���ӳ����ϣ���GA=GE��
��1����֤��AG���O���У�
��2����AC=6��AB=8��BE=3�����߶�OE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������9�֣���ͼ����OΪRt��ABCб��AB�ϵ�һ�㣬��OAΪ�뾶����O��BC���ڵ�D����AC���ڵ�E������AD��

��1����֤��ADƽ����BAC��
��2������BAC = 60����OA = 2������Ӱ���ֵ�������������![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018������������������2018��5��27���ڳ����о��У�����10����������dz����������ģ��յ������ǹ㳡���������������Ͼ������5km������һ������վ���������7.5km������һ��ʳƷ����վ��С�������μ���10��������Ŀ��Ϊ�˸��õ���ɱ�����С���ڱ���ǰ������һ��ģ���ܣ����������������������յ㣬С����������ǰ��̺��ٶ�������![]() ����������������̣�С�����յ�֮���·��
����������������̣�С�����յ�֮���·��![]() ��ʱ��
��ʱ��![]() ֮��ĺ���ͼ����ͼ��ʾ������ͼ����Ϣ������������⣮(1����=1ǧ��)
֮��ĺ���ͼ����ͼ��ʾ������ͼ����Ϣ������������⣮(1����=1ǧ��)
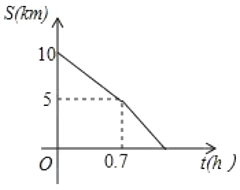
��1��С������������ܵ�����վ���ٶ�Ϊ_______![]() ��С������ȫ������ʱ��Ϊ________
��С������ȫ������ʱ��Ϊ________![]() ��
��
��2����С��������վ�ܵ��յ�Ĺ�����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��3����С��������ܵ�ʳƷ����վ����ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�ּ�NAM�У���A��15�㣬��Ҫ�ڽǵ��ڲ����ϵȳ��ĸ��������ڸ�����β��ӣ����ӹ̸ּܣ���AP1��P1P2��P2P3�������������ĸ������ֻ�ܺ��ϣ�����������
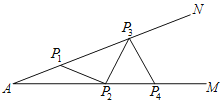
A.4B.5C.6D.7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijũ���а���ɽ����44��ƻ���������ڽ���������ջ��ڣ��ջ�ʱ��������ժ��5�����ϵ�ƻ�����Ƶ�ÿ����ժ�õ�ƻ���������£���λ��ǧ�ˣ�35 35 34 39 37
(1)����������У�����ָ���ǣ�����ָ���ǣ������ǣ����������ǣ�
(2)�Ը�������ƽ����ȥ�����������������Ϊ��ũ�����ջ�ƻ����Լ����ǧ�ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ABC����������A��B��C���Եı߷ֱ�Ϊa��b��c����ô���������У������ж���ABC��ֱ�������ε��ǣ�������
A.��A��25������B��65��B.��A����B����C��2��3��5
C.a��b��c��![]() ��
��![]() ��
��![]() D.a��6��b��10��c��12
D.a��6��b��10��c��12
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com