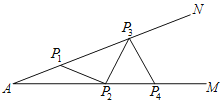
【题目】如图，一钢架NAM中，∠A＝15°，现要在角的内部焊上等长的钢条（相邻钢条首尾相接）来加固钢架．如AP1＝P1P2＝P2P3＝…，则这样的钢条最多只能焊上（ ）根．
A.4B.5C.6D.7
【答案】B
【解析】
由于P1A＝P1P2，利用三角形外角性质，易得∠2，而P2P1＝P2P3，又易求∠P1P2P3＝120°，以此类推，易求∠P3P5P6＝90°，根据邻补角性质可知∠P6P5M＝90°，若再焊接，那么出来的三角形的底角就有两个是90°，不符合三角形内角和定理，故只能焊接5根．
如图，
∵P1A＝P1P2，
∴∠A＝∠1＝15°，
∴∠2＝30°，
∵P2P1＝P2P3，
∴∠3＝∠2＝30°，
∴∠P1P2P3＝120°，
…
易知∠6＝∠7＝60°，∠8＝∠9＝75°，
∴∠P4P5P6＝30°，
∴∠P3P5P6＝90°，
∴∠P6P5M＝90°，
那么第6个三角形将有两个底角等于90°，不符合三角形内角和定理，故只能焊5根．
故选：B．
走进文言文系列答案科目：初中数学 来源： 题型：
【题目】已知：如图，抛物线y=﹣x2+bx+c与x轴交于点A（﹣1，0），B（3，0），与y轴交于点C．过点C作CD∥x轴，交抛物线的对称轴于点D．
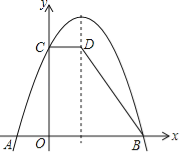
（1）求该抛物线的解析式；
（2）若将该抛物线向下平移m个单位，使其顶点落在D点，求m的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，已知抛物线y=﹣x2﹣4x+5交x轴于点A、B两点（点A在点B的左侧），交y轴于点C，点D为抛物线的顶点，连接AD．
（1）求直线AD的解析式．
（2）点E（m，0）、F（m+1，0）为x轴上两点，其中（﹣5＜m＜﹣3.5）EE′、FF′分别平行于y轴，交抛物线于点E′和F′，交AD于点M、N，当ME′+NF′的值最大时，在y轴上找一点R，使得|RE′﹣RF′|值最大，请求出点R的坐标及|RE′﹣RF′|的最大值．
（3）如图2，在抛物线上是否存在点P，使得△PAC是以AC为底边的等腰三角形，若存在，请出点P的坐标及△PAC的面积，若不存在，请说明理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y1=﹣x+4，y2=
x+b都与双曲线y=
交于点A（1，m），这两条直线分别与x轴交于B，C两点．
（1）求y与x之间的函数关系式；
（2）直接写出当x＞0时，不等式x+b＞的解集；
（3）若点P在x轴上，连接AP把△ABC的面积分成1：3两部分，求此时点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】 如图，在直角坐标系中，矩形OABC的顶点O在坐标原点，边OA在x轴上，
OC在y轴上，如果矩形OA′B′C′与矩形OABC关于点O位似，且矩形OA′B′C′的面积等于矩形OABC面积的
，那么点B′的坐标是【 】
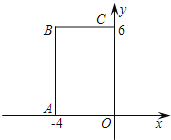
A．（－2，3） B．（2，－3） C．（3，－2）或（－2，3） D．（－2，3）或（2，－3）
查看答案和解析>>
科目：初中数学 来源： 题型：
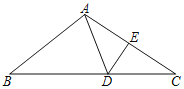
【题目】如图，△ABC的周长为30cm，把△ABC的边AC对折，使顶点A和C重合，折痕交BC边于点D，交AC边于点E，若△ABD的周长是22cm，则AE的长为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
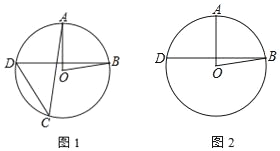
【题目】如图，在⊙O中，半径OA与弦BD垂直，点C在⊙O上，∠AOB＝80°
（1）若点C在优弧BD上，求∠ACD的大小；
（2）若点C在劣弧BD上，直接写出∠ACD的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
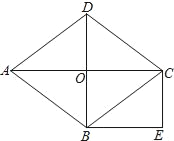
【题目】如图，O是菱形ABCD对角线AC与BD的交点，CD=5cm，OD=3cm；过点C作CE∥DB，过点B作BE∥AC，CE与BE相交于点E．
（1）求OC的长；
（2）求四边形OBEC的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
