
【题目】已知:如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.过点C作CD∥x轴,交抛物线的对称轴于点D.
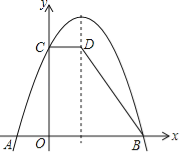
(1)求该抛物线的解析式;
(2)若将该抛物线向下平移m个单位,使其顶点落在D点,求m的值.
 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】(1)计算:2﹣1+(π﹣3.14)0+sin60°﹣|﹣![]() |
|
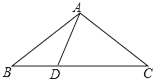
(2)如图,在△ABC中,AB=AC=10,sinC=![]() ,点D是BC上一点,且DC=AC.求BD的长.
,点D是BC上一点,且DC=AC.求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班部分学生接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了如图①②两幅不完整的统计图,请根据图中的信息解答下列问题.
(1)九年级(1)班接受调查的学生共有多少名?
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
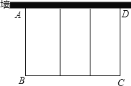
【题目】如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成三个大小相同的矩形羊圈.
(1)若羊圈总面积为400平方米,求羊圈的边长AB, BC各为多少米?
(2) 保持羊圈的基本结构,求羊圈总面积最大可以是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
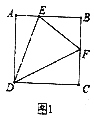
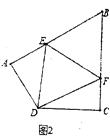
【题目】(1)如图①,四边形![]() 为正方形,点
为正方形,点![]() 分别在
分别在![]() 与
与![]() 上,且
上,且![]() ,求证:
,求证:![]() .
.
(2)如图②,在四边形![]() 中,
中,![]() ,点
,点![]() 分别在
分别在![]() 与
与![]() 上,且
上,且![]() .猜想
.猜想![]() 与
与![]() 之间的数量关系,并证明你的猜想;
之间的数量关系,并证明你的猜想;
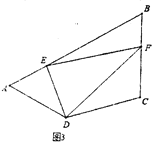
(3)如图③,在四边形![]() 中,
中,![]() 与
与![]() 互补,点
互补,点![]() 分别在
分别在![]() 与
与![]() 上,且
上,且![]() ,请直接写出
,请直接写出![]() ,
,![]() 与
与![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用无刻度的直尺按要求作图,请保留画图痕迹,不需要写作法。
(1)在8×6的正方形网格中,请用无刻度直尺画一个![]() 与
与![]() 面积相等,顶点在格点上 .(画出一个满足条件即可)
面积相等,顶点在格点上 .(画出一个满足条件即可)
(2)在8×6的正方形网格中,请用无刻度直尺画一个与![]() 面积相等,且以
面积相等,且以![]() 为边的平行四边形,顶点在格点上.(画出一个满足条件即可)
为边的平行四边形,顶点在格点上.(画出一个满足条件即可)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】烟台享有“苹果之乡”的美誉.甲、乙两超市分别用3000元以相同的进价购进质量相同的苹果.甲超市销售方案是:将苹果按大小分类包装销售,其中大苹果400千克,以进价的2倍价格销售,剩下的小苹果以高于进价10%销售.乙超市的销售方案是:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利2100元(其它成本不计).问:
(1)苹果进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
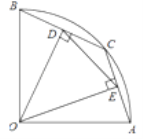
【题目】如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧 AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为点D,E;在点C的运动过程中,下列说法正确的是( )
A. 扇形AOB的面积为![]() B. 弧BC的长为
B. 弧BC的长为![]() C. ∠DOE=45° D. 线段DE的长是
C. ∠DOE=45° D. 线段DE的长是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
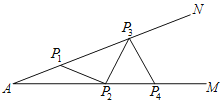
【题目】如图,一钢架NAM中,∠A=15°,现要在角的内部焊上等长的钢条(相邻钢条首尾相接)来加固钢架.如AP1=P1P2=P2P3=…,则这样的钢条最多只能焊上( )根.
A.4B.5C.6D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com