
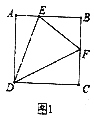
【题目】(1)如图①,四边形![]() 为正方形,点
为正方形,点![]() 分别在
分别在![]() 与
与![]() 上,且
上,且![]() ,求证:
,求证:![]() .
.
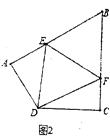
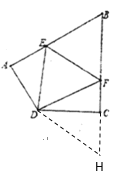
(2)如图②,在四边形![]() 中,
中,![]() ,点
,点![]() 分别在
分别在![]() 与
与![]() 上,且
上,且![]() .猜想
.猜想![]() 与
与![]() 之间的数量关系,并证明你的猜想;
之间的数量关系,并证明你的猜想;
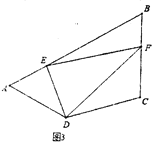
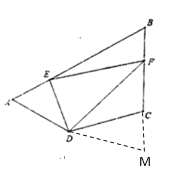
(3)如图③,在四边形![]() 中,
中,![]() 与
与![]() 互补,点
互补,点![]() 分别在
分别在![]() 与
与![]() 上,且
上,且![]() ,请直接写出
,请直接写出![]() ,
,![]() 与
与![]() 之间的数量关系.
之间的数量关系.
【答案】(1)见解析;(2)![]() ,详见解析;(3)
,详见解析;(3)![]() ,详见解析
,详见解析
【解析】
(1)延长至点G,使AG=CF,根据正方形的性质证明△ADG≌△CDF,得到∠ADG=∠CDF,DG=DF,再证明△DEG≌△DEF,即可得到结论;
(2)延长BC至点H,使CH=AE,连接DH,同(1)的方法证明即可得到结论;
(3)![]() ,延长BC至点M,使CM=AE,连接DM,同上的证明方法即可得到结论.
,延长BC至点M,使CM=AE,连接DM,同上的证明方法即可得到结论.
(1)如图,延长至点G,使AG=CF,连接DG,
∵四边形![]() 为正方形,
为正方形,
∴AD=CD,∠BAD=∠ADC=∠C=90°,
∴△ADG≌△CDF,
∴∠ADG=∠CDF,DG=DF,
∵![]() ,
,
∴∠ADG+∠CDF=∠ADE+∠CDF=45°,
∵DE=DE,
∴△DEG≌△DEF,
∴EF=GE=AG+AE=CF+AE,
∴![]() ;
;
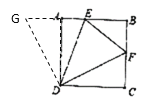
(2)AE+CF=EF,
延长BC至点H,使CH=AE,连接DH,
∵∠A=∠BCD=90°,
∴∠A=∠DCH=90°,
∵AD=CD,AE=CH,
∴△ADE≌△CDH,
∴DE=DH,∠ADE=∠CDH,
∵∠ADC=120°,
∴∠EDH=120°,
∵∠EDF=60°,
∴∠HDF=∠EDF=60°,
又∵CD=CD,
∴△EDF≌△HDF,
∴EF=HF=CF+CH=AE+CF;
(3)![]() ,
,
延长BC至点M,使CM=AE,连接DM,
∵∠DAB与∠BCD互补,
∴∠DAB+∠BCD==180°,
∴∠DAB=∠DCM,
∵AD=CD,AE=CM,
∴△ADE≌△CDM,
∴DE=DM,∠ADE=∠CDM,
∵![]() ,
,![]() ,
,
∴∠MDF=![]() ,
,
又∵DF=DF,
∴△EDF≌△MDF,
∴EF=MF=CM+CF=AE+CF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在□ABCD 中,对角线 AC 与 BD 相交于点 O ,点 E , F 分别为 OB , OD 的中点,延长 AE 至 G ,使 EG =AE ,连接 CG .
(1)求证: △ABE≌△CDF ;
(2)当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
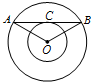
【题目】如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于点C,若∠AOB=120°,则大圆半径R与小圆半径r之间满足( )
A、![]() B、R=3r
B、R=3r
C、R=2rD、![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人参加从![]() 地到
地到![]() 地的长跑比赛,两人在比赛时所跑的路程
地的长跑比赛,两人在比赛时所跑的路程![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系如图所示,请你根据图象,回答下列题:
(分钟)之间的函数关系如图所示,请你根据图象,回答下列题:
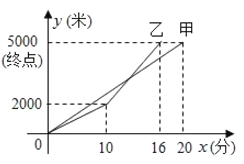
(1)________(填“甲”或“乙”)先到达终点;甲的速度是________米/分钟;
(2)求甲与乙相遇时,他们离![]() 地多少米?
地多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.过点C作CD∥x轴,交抛物线的对称轴于点D.
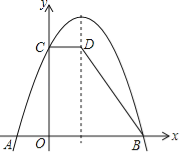
(1)求该抛物线的解析式;
(2)若将该抛物线向下平移m个单位,使其顶点落在D点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某市开展的环境创优活动中,某居民小区要在一块靠墙(墙长15米)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成,若设花园平行于墙的一边长为x(m),花园的面积为y(m2).
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)满足条件的花园面积能达到200m2吗?若能,求出此时x的值,若不能,说明理由;
(3)根据(1)中求得的函数关系式,判断当x取何值时,花园的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
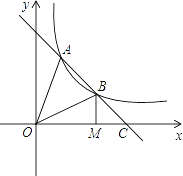
【题目】如图,直线AB交双曲线 ![]() 于A,B两点,交x轴于点C,且BC=
于A,B两点,交x轴于点C,且BC= ![]() AB,过点B作BM⊥x轴于点M,连结OA,若OM=3MC,S△OAC=8,则k的值为多少?
AB,过点B作BM⊥x轴于点M,连结OA,若OM=3MC,S△OAC=8,则k的值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com