
【题目】甲、乙两人参加从![]() 地到
地到![]() 地的长跑比赛,两人在比赛时所跑的路程
地的长跑比赛,两人在比赛时所跑的路程![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系如图所示,请你根据图象,回答下列题:
(分钟)之间的函数关系如图所示,请你根据图象,回答下列题:
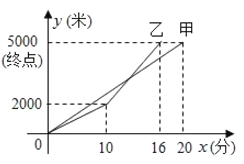
(1)________(填“甲”或“乙”)先到达终点;甲的速度是________米/分钟;
(2)求甲与乙相遇时,他们离![]() 地多少米?
地多少米?
科目:初中数学 来源: 题型:
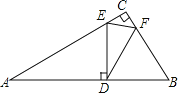
【题目】如图,在一块直角三角板ABC中,∠C=90°,∠A=30°,BC=1,将另一个含30°角的△EDF的30°角的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直,若△CEF与△DEF相似,则AD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
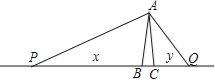
【题目】如图,在△ABC中,AB=AC=2,∠BAC=20°.动点P、Q分别在直线BC上运动,且始终保持∠PAQ=100°.设BP=x,CQ=y,则y与x之间的函数关系用图象大致可以表示为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
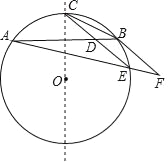
【题目】如图所示AB为⊙O的一条弦,点C为劣弧AB的中点,E为优弧AB上一点,点F在AE的延长线上,且BE=EF,线段CE交弦AB于点D.
(1)求证:CE∥BF;
(2)若BD=2,且EA:EB:EC=3:1:![]() ,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲进行了10次射苦练,平均成绩为9环,且前9次的成绩(单位:环)依次为:8,10,9,10,7,9,10,8,10.
(1)求甲第10次的射击成绩:
(2:求甲这10次射击成绩的方差:
(3)乙在相同情况下也进行了10次射击训练,平均成绩为9环,方差为1.6环,请问从甲和乙两个人中选一个去参加比赛,你认为哪个去更合适?并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
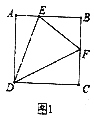
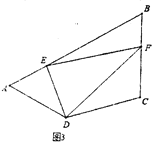
【题目】(1)如图①,四边形![]() 为正方形,点
为正方形,点![]() 分别在
分别在![]() 与
与![]() 上,且
上,且![]() ,求证:
,求证:![]() .
.
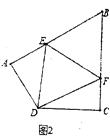
(2)如图②,在四边形![]() 中,
中,![]() ,点
,点![]() 分别在
分别在![]() 与
与![]() 上,且
上,且![]() .猜想
.猜想![]() 与
与![]() 之间的数量关系,并证明你的猜想;
之间的数量关系,并证明你的猜想;
(3)如图③,在四边形![]() 中,
中,![]() 与
与![]() 互补,点
互补,点![]() 分别在
分别在![]() 与
与![]() 上,且
上,且![]() ,请直接写出
,请直接写出![]() ,
,![]() 与
与![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
①EG=DF;
②∠AEH+∠ADH=180°;
③△EHF≌△DHC;
④若![]() ,则S△EDH=13S△CFH .
,则S△EDH=13S△CFH .

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com