
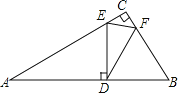
【题目】如图,在一块直角三角板ABC中,∠C=90°,∠A=30°,BC=1,将另一个含30°角的△EDF的30°角的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直,若△CEF与△DEF相似,则AD= .
【答案】![]() 或
或![]()
【解析】
试题由于∠EDF=30°,且DE总垂直于AB,因此∠FDB=60°,此时发现△FDB是等边三角形,那么BD=BF,2﹣AD=1﹣CF,即AD=CF+1.由于∠C是直角,当△CEF与△DEF相似时,△DEF必为直角三角形,那么可分两种情况讨论:①∠DEF=90°,此时,△CEF∽△DEF;②∠DFE=90°,此时△CEF∽△FED;可根据各相似三角形得到的比例线段求出CF的值,进而可求得AD的值.
解:∵∠EDF=30°,ED⊥AB于D,
∴∠FDB=∠B=60°,
∴△BDF是等边三角形;
∵BC=1,∴AB=2;
∵BD=BF,
∴2﹣AD=1﹣CF;
∴AD=CF+1.
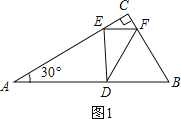
①如图1,∠FED=90°,△CEF∽△EDF,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,CF=![]() ;
;
∴AD=![]() +1=
+1=![]() ;
;
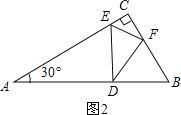
②如图2,∠EFD=90°,△CEF∽△FED,
∴![]() =
=![]() ,即
,即![]() =
=![]() ;
;
解得,CF=![]() ;
;
∴AD=![]() +1=
+1=![]() .
.
故答案为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图是盼盼家新装修的房子,其中三个房间甲、乙、丙.他将一个梯子斜靠在墙上,梯子顶端距离地面的垂直距离记作![]() ,如果梯子的底端
,如果梯子的底端![]() 不动,顶端靠在对面墙上,此时梯子的顶端距离地面的垂直距离记作
不动,顶端靠在对面墙上,此时梯子的顶端距离地面的垂直距离记作![]() .
.
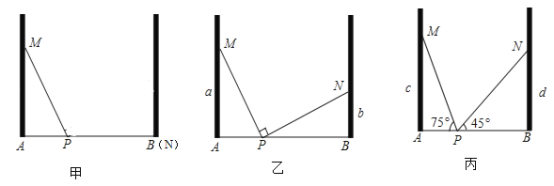
(1)当盼盼在甲房间时,梯子靠在对面墙上,顶端刚好落在对面墙角![]() 处,若
处,若![]() 米,
米,![]() 米,则甲房间的宽
米,则甲房间的宽![]() ______米;
______米;
(2)当盼盼在乙房间时,测得![]() 米,
米,![]() 米,且
米,且![]() ,求乙房间的宽
,求乙房间的宽![]() ;
;
(3)当盼盼在丙房间时,测得![]() 米,且
米,且![]() ,
,![]() .
.
①求![]() 的度数;
的度数;
②求丙房间的宽![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的内接四边形ABCD中,AC,BD是它的对角线,AC的中点I是△ABD的内心.求证:
(1)OI是△IBD的外接圆的切线;
(2)AB+AD=2BD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CG=EG
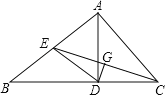
(1)求证:CD=AE;
(2)若AD=BD,CD=2,则求△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,AB=6,BC=8,E,F分别是AB,BC的中点,AF与DE相交于I,与BD相交于H,则四边形BEIH的面积为( )
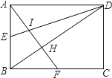
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD 中,对角线 AC 与 BD 相交于点 O ,点 E , F 分别为 OB , OD 的中点,延长 AE 至 G ,使 EG =AE ,连接 CG .
(1)求证: △ABE≌△CDF ;
(2)当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点.
点.
(1)求![]() 的取值范围;
的取值范围;
(2)若![]() ,直线
,直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,求抛物线的解析式;
,求抛物线的解析式;
(3)若![]() 点在
点在![]() 点左边,在第一象限内,(2)中所得到抛物线上是否存在一点
点左边,在第一象限内,(2)中所得到抛物线上是否存在一点![]() ,使直线
,使直线![]() 分
分![]() 的面积为
的面积为![]() 两部分?若存在,求出
两部分?若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣ax﹣2a(a为常数且不等于0)与x轴的交点为A,B两点,且A点在B的右侧.
(1)当抛物线经过点(3,8),求a的值;
(2)求A、B两点的坐标;
(3)若抛物线的顶点为M,且点M到x轴的距离等于AB的3倍,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人参加从![]() 地到
地到![]() 地的长跑比赛,两人在比赛时所跑的路程
地的长跑比赛,两人在比赛时所跑的路程![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系如图所示,请你根据图象,回答下列题:
(分钟)之间的函数关系如图所示,请你根据图象,回答下列题:
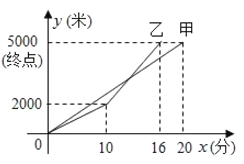
(1)________(填“甲”或“乙”)先到达终点;甲的速度是________米/分钟;
(2)求甲与乙相遇时,他们离![]() 地多少米?
地多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com