
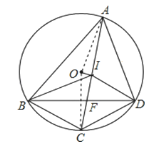
【题目】如图,⊙O的内接四边形ABCD中,AC,BD是它的对角线,AC的中点I是△ABD的内心.求证:
(1)OI是△IBD的外接圆的切线;
(2)AB+AD=2BD.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据三角形内心的性质和同弧上圆周角的性质,以及等角对等边即可证得C是△IBD的外心,然后证得OI⊥CI,即可证得OI是△IBD的外接圆的切线;
(2)根据(1)可以得到AI=CD,AB=2BF,即可证得.
(1)∵∠CID=∠IAD+∠IDA,∠CDI=∠CDB+∠BDI=∠BAC+∠IDA=∠IAD+∠IDA
∴∠CID=∠CDI,
∴CI=CD.
同理,CI=CB.
故点C是△IBD的外心.
连接OA,OC,
∵I是AC的中点,且OA=OC,
∴OI⊥AC,即OI⊥CI.
∴OI是△IBD外接圆的切线.
(2)由(1)可得:
∵AC的中点I是△ABD的内心,
∴∠BAC=∠CAD
∴∠BDC=∠DAC=∠BAC,
又∵∠ACD=∠DCF,
∴△ADC∽△DFC,
∴![]() ,
,
∵AC=2CI
∴AC=2CD
∴AD=2DF
同理可得:AB=2BF
∴AB+AD=2BF+2DF=2BD.


科目:初中数学 来源: 题型:
【题目】(12分)某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元![]() ,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式(不要求写自变量的取值范围);
,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式(不要求写自变量的取值范围);
(2)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC且tanA= ![]() ,P为BC上一点,且BP:PC=3:5,E、F分别为AB、AC上的点,且∠EPF=2∠B,若△EPF的面积为6,则EF=________.
,P为BC上一点,且BP:PC=3:5,E、F分别为AB、AC上的点,且∠EPF=2∠B,若△EPF的面积为6,则EF=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
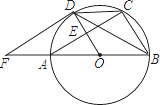
【题目】如图,AB是⊙O的直径,AC是弦,半径OD⊥AC于点E,过点D的切线与BA延长线交于点F.
(1)求证:∠CDB=∠BFD;
(2)若AB=10,AC=8,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点D为![]() 内部(包括边界但非A、B、C)上的一点.
内部(包括边界但非A、B、C)上的一点.

(1)若点D在边AC上,如图①,求证:AB + AC> BD + DC
(2)若点D在![]() 内,如图②,求证:AB + AC> BD + DC
内,如图②,求证:AB + AC> BD + DC
(3)若点D在![]() 内,连结DA、DB、DC,如图③求证:
内,连结DA、DB、DC,如图③求证:![]() (AB + BC + AC) < DA + DB + DC < AB + BC + AC
(AB + BC + AC) < DA + DB + DC < AB + BC + AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
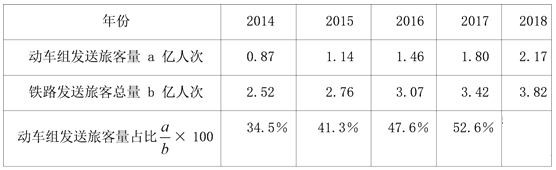
【题目】随着高铁的建设,春运期间动车组发送旅客量越来越大,相关部门为了进一步了解春运期间动车组发送旅客量的变化情况,针对2014年至2018年春运期间的铁路发送旅客量情况进行了调查,过程如下.
(Ⅰ)收集、整理数据
请将表格补充完整:
(Ⅱ)描述数据
为了更直观地显示动车组发送旅客量占比的变化趋势,需要用什么图(回答“折线图”或“扇形图”)进行描述;
(Ⅲ)分析数据、做出推测
预估2019年春运期间动车组发送旅客量占比约为多少,说明你的预估理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com