
【题目】如图,菱形OABC,A点的坐标为(5,0),对角线OB、AC相交于D点,双曲线y=![]() (x>0)经过D点,交BC的延长线于E点,交AB于F点,连接OF交AC于M,且OBAC=40.有下列四个结论:①k=8;②CE=1;③AC+OB=6
(x>0)经过D点,交BC的延长线于E点,交AB于F点,连接OF交AC于M,且OBAC=40.有下列四个结论:①k=8;②CE=1;③AC+OB=6![]() ;④S△AFM:S△AOM=1:3.其中正确的结论是( )
;④S△AFM:S△AOM=1:3.其中正确的结论是( )
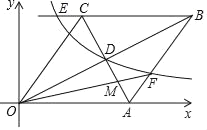
A. ①②B. ①③C. ①②③D. ①②③④
【答案】D
【解析】
首先过点D作DH⊥x轴于点H,由菱形OABC中,ACOB=40,可求得菱形OABC的面积,继而求得△AOD的面积,则可求得高DH,然后由射影定理,可得DH2=OHAH,继而求得①正确;过C作CG⊥x轴于点G,根据平行线等分线段定理和三角形的中位线的性质得到CG=2DH=4,AG=2AH=2,求得C(3,4),E(2,4),于是得到CE=1,故②正确;根据勾股定理得到AC+OB=6![]() ;故③正确;过F作FN⊥x轴于点N,设FN=4x,AN=3x,根据三角形的面积公式得到x=
;故③正确;过F作FN⊥x轴于点N,设FN=4x,AN=3x,根据三角形的面积公式得到x=![]() ,根据相似三角形的性质得到
,根据相似三角形的性质得到![]() ,于是得到S△AFM:S△AOM=1:3,故④正确.
,于是得到S△AFM:S△AOM=1:3,故④正确.
解:过点D作DH⊥x轴于点H,
∵菱形OABC中,ACOB=40,
∴S菱形OABC=![]() ACOB=20,
ACOB=20,
∴S△OAD=![]() S菱形OABC=5,
S菱形OABC=5,
∵S△OAD=![]() OADH,且OA=5,
OADH,且OA=5,
∴DH=2,
∵DH2=OHAH=4,OH+AH=5,
∴OH=4,AH=1,
∴点D(4,2),
∴k=4×2=8.故①正确;
过C作CG⊥x轴于点G,
∴DH∥CG,
∵AD=CD,
∴CG=2DH=4,AG=2AH=2,
∴OG=3,
∴C(3,4),
∴E(2,4),
∴CE=1,故②正确;
∵CG=4,AG=2,
∴AC=![]() =2
=2![]() ,
,
∵DH=2,OH=4,
∴OD=2![]() ,
,
∴OB=4![]() ,
,
∴AC+OB=6![]() ;故③正确;
;故③正确;
过F作FN⊥x轴于点N,
∵OC∥AB,
∴∠COG=∠FAN,
∴tan∠COG=tan∠FAN=![]() =
=![]() =
=![]() ,
,
设FN=4x,AN=3x,
∴S△OFN=![]() (5+3x)×4x=4,
(5+3x)×4x=4,
∴x=![]() ,
,
∴FN=![]() ,AN=1,
,AN=1,
∵△OCG∽△AFN,
∴![]() =3,
=3,
∵OC∥AF,
∴△AMF∽△CMO,
∴![]() =3,
=3,
∴S△AFM:S△AOM=1:3,故④正确,
故选:D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中有2个完全相同的小球,分别标有数字0和-2;乙袋中有3个完全相同的小球,分别标有数字-2,0和1,小明从甲袋中随机取出1个小球,记录标有的数字为x,再从乙袋中随机取出1个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y).
(1)写出点Q所有可能的坐标;
(2)求点Q在x轴上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知A(2,0),B(1,-1),将线段OA绕点O逆时针旋转,旋转角为![]() (0°<
(0°<![]() <135°).记点A的对应点为A1,若点A1与点B的距离为
<135°).记点A的对应点为A1,若点A1与点B的距离为![]() ,则
,则![]() 为( ).
为( ).
A. 30° B. 45° C. 60° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间![]() (单位:小时),将学生分成五类:
(单位:小时),将学生分成五类: ![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),绘制成尚不完整的条形统计图如图11.
),绘制成尚不完整的条形统计图如图11.

根据以上信息,解答下列问题:
(1)![]() 类学生有 人,补全条形统计图;
类学生有 人,补全条形统计图;
(2)![]() 类学生人数占被调查总人数的 %;
类学生人数占被调查总人数的 %;
(3)从该班做义工时间在![]() 的学生中任选2人,求这2人做义工时间都在
的学生中任选2人,求这2人做义工时间都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
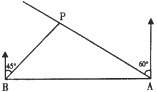
【题目】如图,在一笔直的海岸线上有A,B两个观测站,A在B的正东方向,有一艘小船停在点P处,从A测得小船在北偏西60°的方向,从B测得小船在北偏东45°的方向,BP=6![]() km.
km.
(1)求A、B两观测站之间的距离;
(2)小船从点P处沿射线AP的方向前行,求观测站B与小船的最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣![]() x+3与x轴、y轴分别相交于点A、B,再将△A0B沿直钱CD折叠,使点A与点B重合.折痕CD与x轴交于点C,与AB交于点D.
x+3与x轴、y轴分别相交于点A、B,再将△A0B沿直钱CD折叠,使点A与点B重合.折痕CD与x轴交于点C,与AB交于点D.
(1)点A的坐标为 ;点B的坐标为 ;
(2)求OC的长度,并求出此时直线BC的表达式;
(3)直线BC上是否存在一点M,使得△ABM的面积与△ABO的面积相等?若存在,请直接写出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC为⊙O的直径,以BC为直角边作Rt△ABC,∠ACB=90°,斜边AB与⊙O交于点D,过点D作⊙O的切线DE交AC于点E,DG⊥BC于点F,交⊙O于点G.

(1)求证:AE=CE;
(2)若AD=4,AE=![]() ,求DG的长.
,求DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
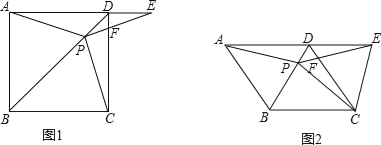
【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com