
【题目】已知抛物线y=ax2+bx+c的顶点为D(﹣1,3),与x轴的一个交点在(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:
①b2+4ac>0;②c﹣a=3;③a+b+c<0;④方程ax2+bx+c=m(m≥2)一定有实数根,其中正确的结论为( )
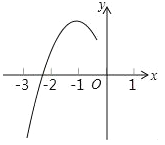
A.②③ B.①③ C.①②③ D.①②④
【答案】C
【解析】
试题分析:∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,所以①正确;
∵抛物线的顶点为D(﹣1,3),
∴a﹣b+c=3,
∵抛物线的对称轴为直线x=﹣![]() =﹣1,
=﹣1,
∴b=2a,
∴a﹣2a+c=3,即c﹣a=3,所以②正确;
∵抛物线的对称轴为直线x=﹣1,
∵抛物线与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,
∴抛物线与x轴的另一个交点在点(0,0)和(1,0)之间,
∴当x=1时,y<0,
∴a+b+c<0,所以③正确;
∵抛物线的顶点为D(﹣1,3),
∵当x=﹣1时,二次函数有最大值为3,
∴方程ax2+bx+c=3有两个相等的实数根,
∵m≥2,
∴方程ax2+bx+c=m(m>3)没有实数根,所以④错误.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AC、BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=3,则下列结论:①![]() ;②S△BCE=30;③S△ABE=9;④△AEF∽△ACD,其中一定正确的是( )
;②S△BCE=30;③S△ABE=9;④△AEF∽△ACD,其中一定正确的是( )
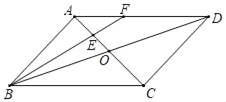
A.①②③④B.①③C.②③④D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为( ).
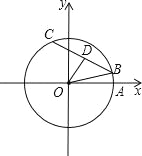
A.22 B.24 C.10![]() D.12
D.12![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:
数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.

理解:
⑴如图![]() ,已知
,已知![]() 是⊙
是⊙![]() 上两点,请在圆上找出满足条件的点
上两点,请在圆上找出满足条件的点![]() ,使
,使![]() 为“智慧三角形”(画出点
为“智慧三角形”(画出点![]() 的位置,保留作图痕迹);
的位置,保留作图痕迹);
⑵如图![]() ,在正方形
,在正方形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 上一点,且
上一点,且![]() ,试判断
,试判断![]() 是否为“智慧三角形”,并说明理由;
是否为“智慧三角形”,并说明理由;
运用:
⑶如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,⊙
中,⊙![]() 的半径为
的半径为![]() ,点
,点![]() 是直线
是直线![]() 上的一点,若在⊙
上的一点,若在⊙![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 为“智慧三角形”,当其面积取得最小值时,直接写出此时点
为“智慧三角形”,当其面积取得最小值时,直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电商平台长期销售A型商品,2017年以4800元购进该型号商品并且全部售完;2019年,这种型号的商品的进价比2017年下降了9元/件,该平台用3000元购进了与2017年相同数量的该A型商品也全部售完,这两年A型商品的售价均为40元/件.
(1)2017年A型商品的进价是多少元/件?
(2)若该电商平台每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知圆0的直径AB垂直于弦CD于点E,CG是圆O的切线交AB的延长线于点G,连接CO并延长交AD于点F,且CF![]() AD.
AD.
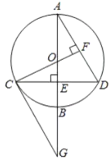
(1)试问:CG//AD吗?说明理由:
(2)证明:点E为OB的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题时,我们常常从特殊入手,猜想结论,并尝试发现解决问题的策略与方法.
(问题提出)
求证:如果一个定圆的内接四边形对角线互相垂直,那么这个四边形的对边的平方和是一个定值.
(从特殊入手)
我们不妨设定圆O的半径是R,⊙O的内接四边形ABCD中,AC⊥BD.
请你在图①中补全特殊殊位置时的图形,并借助于所画图形探究问题的结论.

(问题解决)
已知:如图②,定圆⊙O的半径是R,四边形ABCD是⊙O的内接四边形, AC⊥BD.
求证: .
证明:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点在(﹣3,0和(﹣2,0)之间,其部分图象如图,则下列结论:①2a﹣b=0:②4ac﹣b2<0:③点(x1,y1),(x2,y2)在抛物线上若x1<x2,则y1<y2;④a+b+c<0.正确结论的个数是( )
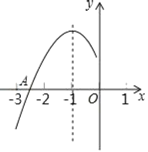
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象与x轴的交点的横坐标分别为﹣1、3,则下列结论:①abc<0;②2a+b=0;③3a+2c>0;④对于任意x均有ax2﹣a+bx﹣b≥0,正确个数有( )
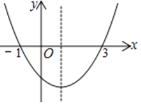
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com