
【题目】如图,在平行四边形ABCD中,AC、BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=3,则下列结论:①![]() ;②S△BCE=30;③S△ABE=9;④△AEF∽△ACD,其中一定正确的是( )
;②S△BCE=30;③S△ABE=9;④△AEF∽△ACD,其中一定正确的是( )
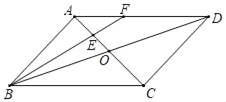
A.①②③④B.①③C.②③④D.①②③
【答案】B
【解析】
根据平行四边形的性质得到AE=![]() CE,根据相似三角形的性质得到比例式,等量代换得到AF=
CE,根据相似三角形的性质得到比例式,等量代换得到AF=![]() AD,于是得到
AD,于是得到![]() ;故①正确;根据相似三角形的性质得到S△BCE=27;故②错误;根据三角形的面积公式得到S△ABE=12,故③正确;由于△AEF与△ADC只有一个角相等,于是得到△AEF与△ACD不一定相似,故④错误.
;故①正确;根据相似三角形的性质得到S△BCE=27;故②错误;根据三角形的面积公式得到S△ABE=12,故③正确;由于△AEF与△ADC只有一个角相等,于是得到△AEF与△ACD不一定相似,故④错误.
解:∵在ABCD中,![]() ,
,
∵点E是OA的中点,
![]() ,
,
∵AD∥BC,
∴△AFE∽△CBE,
![]() ,
,
∵AD=BC,
![]() ,
,
![]() ;故①正确;
;故①正确;
∵S△AEF=3,![]() ,
,
∴S△BCE=27;故②错误;
![]()
![]() ∴S△ABE=9,故③正确;
∴S△ABE=9,故③正确;
∵BF不平行于CD,
∴△AEF与△ADC只有一个角相等,
∴△AEF与△ACD不一定相似,故④错误,
故选B.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】有甲、乙两种糖果,原价分别为每千克a元和b元.根据调查,将两种糖果按甲种糖果x千克与乙种糖果y千克的比例混合,取得了较好的销售效果.现在糖果价格有了调整:甲种糖果单价下降15%,乙种糖果单价上涨20%,但按原比例混合的糖果单价恰好不变,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (
(![]() )的部分图象如图所示,与
)的部分图象如图所示,与![]() 轴的一个交点坐标为
轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() ,下列结论是:①
,下列结论是:①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个不相等的实数根;④
有两个不相等的实数根;④![]() ;⑤若点
;⑤若点![]() 在该抛物线上,则
在该抛物线上,则![]() ,其中正确的个数有( )
,其中正确的个数有( )
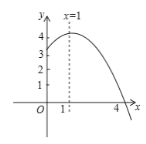
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一条直线截三角形的两边,若所截得的四边形对角互补,则称该直线为三角形第三条边上的逆平行线.如图![]() ,
,![]() 为
为![]() 的截线,截得四边形
的截线,截得四边形![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 边
边![]() 的逆平行线;如图
的逆平行线;如图![]() ,已知
,已知![]() 中,
中,![]() ,过
,过![]() 边上的点
边上的点![]() 作
作![]() 交于点
交于点![]() ,过点
,过点![]() 作边
作边![]() 的逆平行线
的逆平行线![]() ,交
,交![]() 边于点
边于点![]() .
.
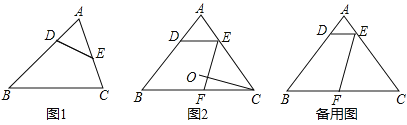
(1)求证:![]() 是边
是边![]() 的逆平行线.
的逆平行线.
(2)![]() 点是
点是![]() 的外心,连接
的外心,连接![]() ,求证:
,求证:![]() .
.
(3)已知![]() ,
,![]() ,过点
,过点![]() 作边
作边![]() 的逆平行线
的逆平行线![]() ,交边
,交边![]() 于点
于点![]() .
.
①试探索![]() 为何值时,四边形
为何值时,四边形![]() 的面积最大,并求出最大值;
的面积最大,并求出最大值;
②在①的条件下,比较![]()
![]() 大小关系.(“
大小关系.(“![]() 或
或![]() ”)
”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织一项公益知识竞赛,比赛规定:每个代表队由3名男生、4名女生和1名指导老师组成.但参赛时,每个代表队只能有3名队员上场参赛,指导老师必须参加,另外2名队员分别在3名男生和4名女生中各随机抽出一名.七年级(1)班代表队有甲、乙、丙三名男生和A、B、C、D4名女生及1名指导老师组成.求:
(1)抽到D上场参赛的概率;
(2)恰好抽到由男生丙、女生C和这位指导老师一起上场参赛的概率.(请用“画树状图”或“列表”的方式给出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校是乒乓球体育传统项目校,为进一步推动该项目的发展.学校准备到体育用品店购买甲、乙两种型号乒乓球若干个,已知3个甲种乒乓球和5个乙种乒乓球共需50元,2个甲种乒乓球和3个乙种乒乓球共需31元.
(1)求1个甲种乒乓球和1个乙种乒乓球的售价各是多少元?
(2)学校准备购买这两种型号的乒乓球共200个,要求甲种乒乓球的数量不超过乙种乒乓球的数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,
上一点,![]() 的平分线交圆
的平分线交圆![]() 于点
于点![]() ,过
,过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,点
,点![]() 是
是![]() 中点,
中点,![]() ,
,![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,点
,点![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() 是等腰三角形;
是等腰三角形;
(3)若![]() ,求
,求![]() 的半径.
的半径.
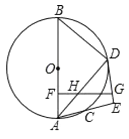
查看答案和解析>>
科目:初中数学 来源: 题型:
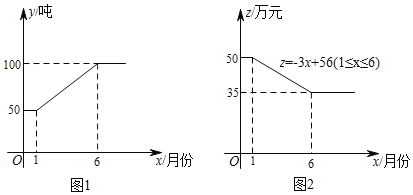
【题目】随着技术的发展进步,某公司2018年采用的新型原料生产产品.这种新型原料的用量y(吨)与月份x之间的关系如图1所示,每吨新型原料所生产的产品的售价z(万元)与月份x之间的关系如图2所示.已知将每吨这种新型原料加工成的产品的成本为20万元.
(1)求出该公司这种新型原料的用量y(吨)与月份x之间的函数关系式;
(2)若该公司利用新型原料所生产的产品当月都全部销售,求哪个月利润最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com