
【题目】如图,已知![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,
上一点,![]() 的平分线交圆
的平分线交圆![]() 于点
于点![]() ,过
,过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,点
,点![]() 是
是![]() 中点,
中点,![]() ,
,![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,点
,点![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() 是等腰三角形;
是等腰三角形;
(3)若![]() ,求
,求![]() 的半径.
的半径.
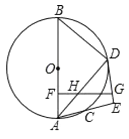
【答案】(1)详见解析;(2)详见解析;(3)![]() 的半径长为8
的半径长为8
【解析】
(1)连接OD,见详解图,通过![]() 的平分线交圆
的平分线交圆![]() 于点
于点![]() 和OD=OA及
和OD=OA及![]() ,易证∠ODE为90°;
,易证∠ODE为90°;
(2)根据FG⊥AO,AD平分∠BAC及∠ADE=90°,易证∠AHF=∠HDG,进而可得∠DHG=∠HDG,即可得出结论;
(3)由![]() 可设
可设![]() ,
,![]() ,则
,则![]() ,因为F为OA中点,所以AF=
,因为F为OA中点,所以AF=![]() ,过G做GM⊥AD,易证
,过G做GM⊥AD,易证![]() ,可得
,可得![]() ,
,![]() ,进而
,进而![]() ,即得答案.
,即得答案.
(1)证明:如图①中,![]() ,∵
,∵![]() ,
,
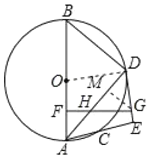
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,∵
,∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的切线;
的切线;
(2)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)∵![]()
设![]() ,
,![]() ,则
,则![]()
∵点![]() 是
是![]() 中点,
中点,
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]() ,
,![]()
![]()
由(2)可知,![]()
过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]() ,
,
∴在![]() 中,
中,![]()
![]()
∴![]()
∴![]()
∴![]() 的半径长为8
的半径长为8


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
【题目】研究发现,二次函数![]() (
(![]() )图象上任何一点到定点(0,
)图象上任何一点到定点(0,![]() )和到定直线
)和到定直线![]() 的距离相等.我们把定点(0,
的距离相等.我们把定点(0,![]() )叫做抛物线
)叫做抛物线![]() 的焦点,定直线
的焦点,定直线![]() 叫做抛物线
叫做抛物线![]() 的准线.
的准线.
(1)写出函数![]() 图象的焦点坐标和准线方程;
图象的焦点坐标和准线方程;
(2)等边三角形OAB的三个顶点都在二次函数![]() 图象上,O为坐标原点,求等边三角形的边长;
图象上,O为坐标原点,求等边三角形的边长;
(3)M为抛物线![]() 上的一个动点,F为抛物线
上的一个动点,F为抛物线![]() 的焦点,P(1,3)为定点,求MP+MF的最小值.
的焦点,P(1,3)为定点,求MP+MF的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AC、BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=3,则下列结论:①![]() ;②S△BCE=30;③S△ABE=9;④△AEF∽△ACD,其中一定正确的是( )
;②S△BCE=30;③S△ABE=9;④△AEF∽△ACD,其中一定正确的是( )
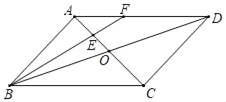
A.①②③④B.①③C.②③④D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Q为正方形ABCD外一点,连接BQ,过点D作DQ⊥BQ,垂足为Q,G、K分别为AB、BC上的点,连接AK、DG,分别交BQ于F、E,AK⊥DG,垂足为点H,AF=5,DH=8,F为BQ中点,M为对角线BD的中点,连接HM并延长交正方形于点N,则HN的长为_____.
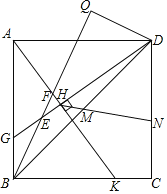
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形![]() 的边
的边![]() 在
在![]() 轴上,点
轴上,点![]() 坐标为
坐标为![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .若将菱形
.若将菱形![]() 向左平移
向左平移![]() 个单位,使点
个单位,使点![]() 落在该反比例函数图象上,则
落在该反比例函数图象上,则![]() 的值为( ).
的值为( ).
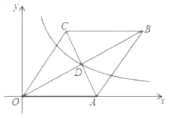
A.1B.2C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是
是![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,过
,过![]() 的延长线上一点
的延长线上一点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,切点为点
,切点为点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
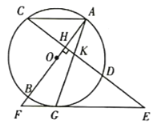
(1)求证:![]() 是等腰三角形;
是等腰三角形;
(2)若![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点P是直线BC上一点,将△BDP沿DP所在的直线翻折后,点B落在B1处,若B1D⊥BC,则点P与点B之间的距离为( )
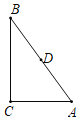
A.1B.![]() C.1或 3D.
C.1或 3D.![]() 或5
或5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com