
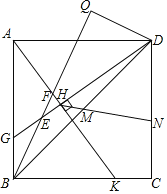
【题目】如图,Q为正方形ABCD外一点,连接BQ,过点D作DQ⊥BQ,垂足为Q,G、K分别为AB、BC上的点,连接AK、DG,分别交BQ于F、E,AK⊥DG,垂足为点H,AF=5,DH=8,F为BQ中点,M为对角线BD的中点,连接HM并延长交正方形于点N,则HN的长为_____.
【答案】![]()
【解析】
由于M是对角线BD中点,因此连接AC,则AC必过M点,且A、H、M、D四点共圆,从而∠DHM=∠MAD=45°,作NP⊥DH于P,则PH=NP,△NPD与△DHA相似,因此只要知道AH与DH之比就可以解决问题了.而DH已知,AF已知,只需求出FH即可.作BR⊥AK于R,连接MR,MF,作MO⊥HR于O,注意到F为BQ中点,于是FM是中位线,由A、M、R、B四点共圆可得△MHR是等腰直角三角形,于是MO=HO=OR,结合△MFO~△FBR,△ABR≌△DAH得到的等量关系可以解出HF的长度,从而求得HN的长度.
连接AC,则AC必过BD中点M.
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠ADC=90°,
作BR⊥AK于R,连接MR,
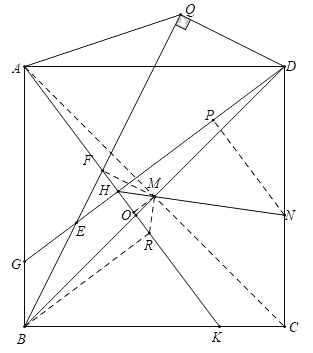
则∠ABR+∠BAR=∠BAR+∠DAH=90°,
∴∠ABR=∠DAH,
∵DG⊥AK于H,
∴∠DHA=∠ARB=90°,
在△ABR和△DAH中:
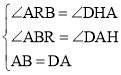
∴△ABR≌△DAH(AAS),
∴BR=AH,AR=DH,
∵正方形对角线AC、BD交于点M,
∴AM=BM=DM,∠BMA=∠AMD=90°,∠MBA=∠MAB=∠MAD=∠MDA=45°,
∴∠BRA=∠BMA,∠AHD=∠AMD,
∴A、B、R、M四点共圆,A、H、M、D四点共圆,
∴∠ARM=∠ABM=45°,∠DHM=∠DAM=45°,
∴∠RHM=∠RHD﹣∠DHM=90°﹣45°=45°,
∴∠RHM=∠HRM=45°,
∴△HMR是等腰直角三角形,
∴OM=OH=OR,
作MO⊥HR,则HO=OR,连接FM,
∵F为BQ中点,
∴FM为△BDQ的中位线,
∴FM∥DQ,
∵DQ⊥BQ,
∴FM⊥BQ,
∴∠BFM=∠BFR+MFO=90°,
又∵∠BFR+∠FBR=90°,
∴∠FBR=∠MFO,
∵∠MOF=∠FRB=90°,
∴△BFR△FMO,
∴![]() =
=![]() ,
,
设FH=x,OM=OH=OR=y,
∵AF=5,DH=8,
∴BR=AH=AF+FH=5+x,AR=DH=AF+FR=5+x+2y=8,
∴FR=x+2y=3,
∴![]() =
=![]() ,
,
解得:x=y=1,
∴AH=AF+x=6,
作NP⊥DG于P,则∠PND+∠PDN=∠PDN+∠ADH=90°,
∴∠ADH=∠PND,
∵∠AHD=∠DPN=90°,
∴△AHD△DPN,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
设PD=3k,PN=4k,
又∵∠DHM=45°,
∴△HPN是等腰直角三角形,
∴PH=PN=4k,HN=![]() PH=4
PH=4![]() k,
k,
∵DH=PD+PH=3k+4k=7k=8,
∴k=![]() ,
,
∴HN=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】日前,某公司决定对塘栖枇杷品种进行培育,育苗基地对其中的四个品种“白砂”“红袍”“夹脚”“宝珠”共500粒种子进行发芽试验,从中选择发芽率最高的品种进行推广,通过实验得知“白砂”品种的发芽率为![]() ,并把实验数据绘成两幅统计图(部分信息未给出):
,并把实验数据绘成两幅统计图(部分信息未给出):
![]()
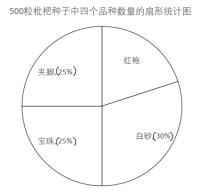
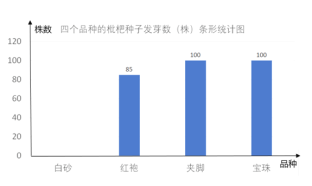
(1)求实验中“红袍”品种的种子数量;
(2)求实验中“白砂”品种的种子发芽的株数,并补全条形统计图;
(3)从以上信息,你认为应选哪一个品种进行推广,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一条直线截三角形的两边,若所截得的四边形对角互补,则称该直线为三角形第三条边上的逆平行线.如图![]() ,
,![]() 为
为![]() 的截线,截得四边形
的截线,截得四边形![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 边
边![]() 的逆平行线;如图
的逆平行线;如图![]() ,已知
,已知![]() 中,
中,![]() ,过
,过![]() 边上的点
边上的点![]() 作
作![]() 交于点
交于点![]() ,过点
,过点![]() 作边
作边![]() 的逆平行线
的逆平行线![]() ,交
,交![]() 边于点
边于点![]() .
.
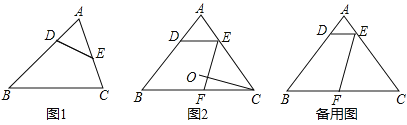
(1)求证:![]() 是边
是边![]() 的逆平行线.
的逆平行线.
(2)![]() 点是
点是![]() 的外心,连接
的外心,连接![]() ,求证:
,求证:![]() .
.
(3)已知![]() ,
,![]() ,过点
,过点![]() 作边
作边![]() 的逆平行线
的逆平行线![]() ,交边
,交边![]() 于点
于点![]() .
.
①试探索![]() 为何值时,四边形
为何值时,四边形![]() 的面积最大,并求出最大值;
的面积最大,并求出最大值;
②在①的条件下,比较![]()
![]() 大小关系.(“
大小关系.(“![]() 或
或![]() ”)
”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织一项公益知识竞赛,比赛规定:每个代表队由3名男生、4名女生和1名指导老师组成.但参赛时,每个代表队只能有3名队员上场参赛,指导老师必须参加,另外2名队员分别在3名男生和4名女生中各随机抽出一名.七年级(1)班代表队有甲、乙、丙三名男生和A、B、C、D4名女生及1名指导老师组成.求:
(1)抽到D上场参赛的概率;
(2)恰好抽到由男生丙、女生C和这位指导老师一起上场参赛的概率.(请用“画树状图”或“列表”的方式给出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校是乒乓球体育传统项目校,为进一步推动该项目的发展.学校准备到体育用品店购买甲、乙两种型号乒乓球若干个,已知3个甲种乒乓球和5个乙种乒乓球共需50元,2个甲种乒乓球和3个乙种乒乓球共需31元.
(1)求1个甲种乒乓球和1个乙种乒乓球的售价各是多少元?
(2)学校准备购买这两种型号的乒乓球共200个,要求甲种乒乓球的数量不超过乙种乒乓球的数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC内接于⊙O,AT切⊙O于点A,AB=BC,且AT∥BC.
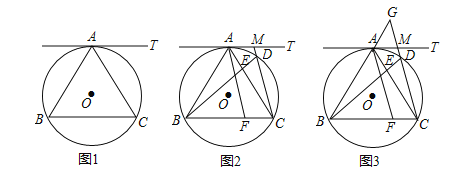
(1)如图1,求证:△ABC是等边三角形;
(2)如图2,点M在射线AT上,连接CM交⊙O于点D,连接BD交AC于点E,AF∥CM交BC于点F,求证:AE=CF;
(3)如图3,在(2)的条件下,延长BA、CM交于点G,若BD=40,CD=25,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,
上一点,![]() 的平分线交圆
的平分线交圆![]() 于点
于点![]() ,过
,过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,点
,点![]() 是
是![]() 中点,
中点,![]() ,
,![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,点
,点![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() 是等腰三角形;
是等腰三角形;
(3)若![]() ,求
,求![]() 的半径.
的半径.
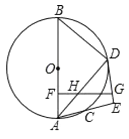
查看答案和解析>>
科目:初中数学 来源: 题型:
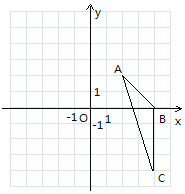
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(2,2),B(4,0),C(4,-4).
(1)请在图中画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴右侧画出△A2B2C2,;
,得到△A2B2C2,请在图中y轴右侧画出△A2B2C2,;
(3)填空:△AA1A2的面积为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
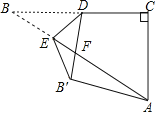
【题目】如图,在Rt△ABC中,∠C=90°,BC=2![]() ,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为_____.
,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com