
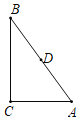
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点P是直线BC上一点,将△BDP沿DP所在的直线翻折后,点B落在B1处,若B1D⊥BC,则点P与点B之间的距离为( )
A.1B.![]() C.1或 3D.
C.1或 3D.![]() 或5
或5
【答案】D
【解析】
分点B1在BC左侧,点B1在BC右侧两种情况讨论,由勾股定理可AB=5,由平行线分线段成比例可得![]() ,可求BE,DE的长,由勾股定理可求PB的长.
,可求BE,DE的长,由勾股定理可求PB的长.
解:如图,若点B1在BC左侧,
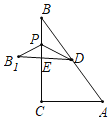
∵∠C=90°,AC=3,BC=4,
∴AB=![]()
∵点D是AB的中点,
∴BD=![]() BA=
BA=![]()
∵B1D⊥BC,∠C=90°
∴B1D∥AC
∴![]()
∴BE=EC=![]() BC=2,DE=
BC=2,DE=![]() AC=
AC=![]()
∵折叠
∴B1D=BD=![]() ,B1P=BP
,B1P=BP
∴B1E=B1D-DE=1
∴在Rt△B1PE中,B1P2=B1E2+PE2,
∴BP2=1+(2-BP)2,
∴BP=![]()
如图,若点B1在BC右侧,
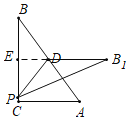
∵B1E=DE+B1D=![]() +
+![]() ,
,
∴B1E=4
在Rt△EB1P中,B1P2=B1E2+EP2,
∴BP2=16+(BP-2)2,
∴BP=5
故选:D.


科目:初中数学 来源: 题型:
【题目】用一条直线截三角形的两边,若所截得的四边形对角互补,则称该直线为三角形第三条边上的逆平行线.如图![]() ,
,![]() 为
为![]() 的截线,截得四边形
的截线,截得四边形![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 边
边![]() 的逆平行线;如图
的逆平行线;如图![]() ,已知
,已知![]() 中,
中,![]() ,过
,过![]() 边上的点
边上的点![]() 作
作![]() 交于点
交于点![]() ,过点
,过点![]() 作边
作边![]() 的逆平行线
的逆平行线![]() ,交
,交![]() 边于点
边于点![]() .
.
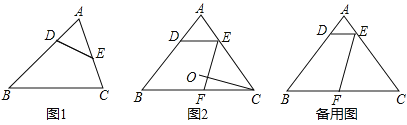
(1)求证:![]() 是边
是边![]() 的逆平行线.
的逆平行线.
(2)![]() 点是
点是![]() 的外心,连接
的外心,连接![]() ,求证:
,求证:![]() .
.
(3)已知![]() ,
,![]() ,过点
,过点![]() 作边
作边![]() 的逆平行线
的逆平行线![]() ,交边
,交边![]() 于点
于点![]() .
.
①试探索![]() 为何值时,四边形
为何值时,四边形![]() 的面积最大,并求出最大值;
的面积最大,并求出最大值;
②在①的条件下,比较![]()
![]() 大小关系.(“
大小关系.(“![]() 或
或![]() ”)
”)
查看答案和解析>>
科目:初中数学 来源: 题型:
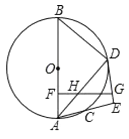
【题目】如图,已知![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,
上一点,![]() 的平分线交圆
的平分线交圆![]() 于点
于点![]() ,过
,过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,点
,点![]() 是
是![]() 中点,
中点,![]() ,
,![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,点
,点![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() 是等腰三角形;
是等腰三角形;
(3)若![]() ,求
,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
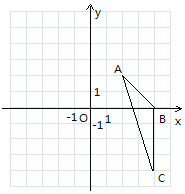
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(2,2),B(4,0),C(4,-4).
(1)请在图中画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴右侧画出△A2B2C2,;
,得到△A2B2C2,请在图中y轴右侧画出△A2B2C2,;
(3)填空:△AA1A2的面积为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂对一批灯泡的质量进行随机抽查,见下表:
抽取灯泡数 | 40 | 100 | 150 | 500 | 1000 | 1500 |
优等品数 | 36 | 92 | 145 | 474 | 950 | 1427 |
优等品频率 |
(1)计算表中的优等品的频率(精确到0.001)
(2)根据抽査的灯泡优等品的频率,估计这批灯泡优等品的概率(精确到0.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三辆汽车经过某收费站下高速时,在2个收费通道A,B中,可随机选择其中的一个通过.
(1)三辆汽车经过此收费站时,都选择A通道通过的概率是 ;
(2)求三辆汽车经过此收费站时,至少有两辆汽车选择B通道通过的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
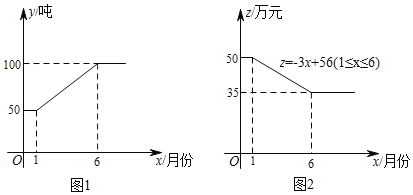
【题目】随着技术的发展进步,某公司2018年采用的新型原料生产产品.这种新型原料的用量y(吨)与月份x之间的关系如图1所示,每吨新型原料所生产的产品的售价z(万元)与月份x之间的关系如图2所示.已知将每吨这种新型原料加工成的产品的成本为20万元.
(1)求出该公司这种新型原料的用量y(吨)与月份x之间的函数关系式;
(2)若该公司利用新型原料所生产的产品当月都全部销售,求哪个月利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
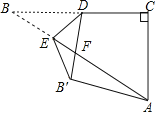
【题目】如图,在Rt△ABC中,∠C=90°,BC=2![]() ,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为_____.
,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
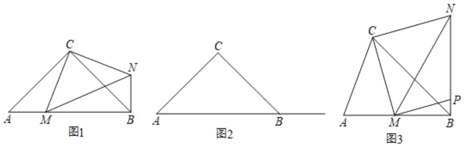
【题目】在△ABC中,∠ABC为锐角,点M为射线AB上一动点,连接CM,以点C为直角顶点,以CM为直角边在CM右侧作等腰直角三角形CMN,连接NB.
(1)如图1,图2,若△ABC为等腰直角三角形,
问题初现:①当点M为线段AB上不与点A重合的一个动点,则线段BN,AM之间的位置关系是 ,数量关系是 ;
深入探究:②当点M在线段AB的延长线上时,判断线段BN,AM之间的位置关系和数量关系,并说明理由;
(2)如图3,∠ACB≠90°,若当点M为线段AB上不与点A重合的一个动点,MP⊥CM交线段BN于点P,且∠CBA=45°,BC=![]() ,当BM= 时,BP的最大值为 .
,当BM= 时,BP的最大值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com