
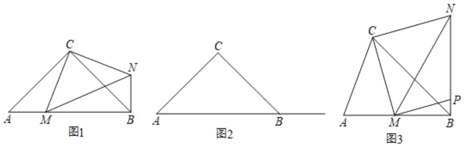
【题目】在△ABC中,∠ABC为锐角,点M为射线AB上一动点,连接CM,以点C为直角顶点,以CM为直角边在CM右侧作等腰直角三角形CMN,连接NB.
(1)如图1,图2,若△ABC为等腰直角三角形,
问题初现:①当点M为线段AB上不与点A重合的一个动点,则线段BN,AM之间的位置关系是 ,数量关系是 ;
深入探究:②当点M在线段AB的延长线上时,判断线段BN,AM之间的位置关系和数量关系,并说明理由;
(2)如图3,∠ACB≠90°,若当点M为线段AB上不与点A重合的一个动点,MP⊥CM交线段BN于点P,且∠CBA=45°,BC=![]() ,当BM= 时,BP的最大值为 .
,当BM= 时,BP的最大值为 .
【答案】(1)①AM⊥BN,AM=BN;②AM与BN位置关系是AM⊥BN,数量关系是AM=BN,见解析;(2)2,1.
【解析】
(1)问题初现:①由“SAS”证明△ACM≌△BCN,可得结论;
深入探究:②由“SAS”证明△ACM≌△BCN,可得结论;
(2)过点C作CE⊥AB于点E,过点N作NF⊥CE于点F,则FN∥AB,通过证明四边形FNBE是矩形,可得CE=BE=4,∠CEM=∠ABN=90°,通过证明△CEM∽△MBP,可得![]() ,即BP=
,即BP=![]() =﹣
=﹣![]() (BM﹣2)2+1,由二次函数的性质可求解.
(BM﹣2)2+1,由二次函数的性质可求解.
解:(1)问题初现:①AM与BN位置关系是AM⊥BN,数量关系是AM=BN.
理由:∵△ABC,△CMN为等腰直角三角形,
∴∠ACB=∠MCN=90°,AC=BC,CM=CN,∠CAB=∠CBA=45°
∴∠ACM=∠BCN,且 AC=BC,CM=CN,
∴△ACM≌△BCN (SAS)
∴∠CAM=∠CBN=45°,AM=BN.
∵∠CAB=∠CBA=45°,
∴∠ABN=45°+45°=90°,即 AM⊥BN
故答案为:AM⊥BN; AM=BN;
深入探究:②当点M在线段AB的延长线上时,AM与BN位置关系是AM⊥BN,数量关系是AM=BN.
理由如下:如图,
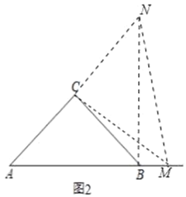
∵△ABC,△CMN为等腰直角三角形,
∴∠ACB=∠MCN=90°,AC=BC,CM=CN,∠CAB=∠CBA=45°
∴∠ACM=∠BCN,且 AC=BC,CM=CN,
∴△ACM≌△BCN (SAS)
∴∠CAM=∠CBN=45°,AM=BN.
∵∠CAB=∠CBA=45°,
∴∠ABN=45°+45°=90°,即 AM⊥BN;
(2)如图,过点C作CE⊥AB于点E,过点N作NF⊥CE于点F,则FN∥AB
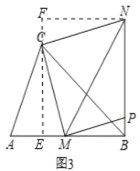
∵△MCN是等腰直角三角形
∴CM=CN,∠MCN=90°
∴∠ECM+∠FCN=90°,且∠ECM+∠CME=90°
∴∠FCN=∠CME,且CM=CN,∠F=∠CEM=90°
∴△CNF≌△CME(AAS)
∴FN=EC,EM=CF
∵BC=![]() ,CE⊥AB,∠CBA=45°
,CE⊥AB,∠CBA=45°
∴CE=BE=4,
∴FN=BE=CE,且FN∥BA
∴四边形FNBE是平行四边形,且∠F=90°
∴四边形FNBE是矩形
∴∠CEM=∠ABN=90°
∴∠PMB+∠MPB=90°
∵CM⊥MP
∴∠CME+∠PMB=90°
∴∠CME=∠MPB,且∠CEM=∠ABN=90°
∴△CEM∽△MBP
∴![]()
∴BP=![]() =﹣
=﹣![]() (BM﹣2)2+1
(BM﹣2)2+1
∴当BM=2时,BP有最大值为1.
故答案为:2,1


科目:初中数学 来源: 题型:
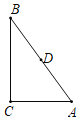
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点P是直线BC上一点,将△BDP沿DP所在的直线翻折后,点B落在B1处,若B1D⊥BC,则点P与点B之间的距离为( )
A.1B.![]() C.1或 3D.
C.1或 3D.![]() 或5
或5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
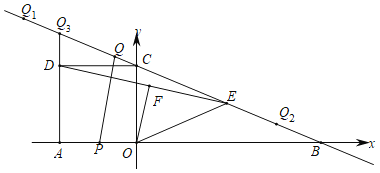
【题目】如图,在平面直角坐标系中,直线![]() 分别交x轴、y轴于点B,C,正方形AOCD的顶点D在第二象限内,E是BC中点,OF⊥DE于点F,连结OE,动点P在AO上从点A向终点O匀速运动,同时,动点Q在直线BC上从某点Q1向终点Q2匀速运动,它们同时到达终点.
分别交x轴、y轴于点B,C,正方形AOCD的顶点D在第二象限内,E是BC中点,OF⊥DE于点F,连结OE,动点P在AO上从点A向终点O匀速运动,同时,动点Q在直线BC上从某点Q1向终点Q2匀速运动,它们同时到达终点.
(1)求点B的坐标和OE的长;
(2)设点Q2为(m,n),当![]() tan∠EOF时,求点Q2的坐标;
tan∠EOF时,求点Q2的坐标;
(3)根据(2)的条件,当点P运动到AO中点时,点Q恰好与点C重合.
①延长AD交直线BC于点Q3,当点Q在线段Q2Q3上时,设Q3Q=s,AP=t,求s关于t的函数表达式.
②当PQ与△OEF的一边平行时,求所有满足条件的AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人加工同一种零件,甲每天加工的数量是乙每天加工数量的 1.5 倍,两人各加工 600 个这种零件,甲比乙少用 5 天.
(1)求甲、乙两人每天各加工多少个这种零件?
(2)已知甲、乙两人加工这种零件每天的加工费分别是 150 元和 120 元,现有 3000 个这种零件的加工任务,甲单独加工一段时间后另有安排,剩余任务由乙单独完成.如果总加工费不超过 7800 元,那么甲至少加工了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:若关于x的一元二次方程ax2+bx+c=0的两个非零实数根分别为x1,x2,则x1+x2=﹣![]() ,x1x2=
,x1x2=![]() .
.
解决下列问题:已知关于x的一元二次方程(x+n)2=6x有两个非零不等实数根x1,x2,设m=![]() ,
,
(Ⅰ)当n=1时,求m的值;
(Ⅱ)是否存在这样的n值,使m的值等于![]() ?若存在,求出所有满足条件的n的值;若不存在,请说明理由.
?若存在,求出所有满足条件的n的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
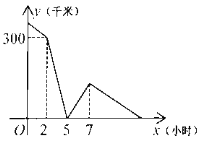
【题目】甲、乙两车分别从A,B两地相向匀速行驶,甲车先出发两小时,甲车到达B地后立即调头,并保持原速度与乙车同向行驶,乙车到达A地后,继续保持原速向远离B的方向行驶,经过一段时间后两车同时到达C地,设两车之间的距离为y(干米),甲车行驶的时间为x小时,y与x之间的函数图象如图所示,则当甲车重返A地时,乙车距离C地________千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某区初二年级数学学科期末质量监控情况,进行了抽样调查,过程如下,请将有关问题补充完整.
收集数据:
随机抽取甲乙两所学校的 20 名学生的数学成绩进行
甲 | 91 | 89 | 77 | 86 | 71 | 31 | 97 | 93 | 72 | 91 |
81 | 92 | 85 | 85 | 95 | 88 | 88 | 90 | 44 | 91 | |
乙 | 84 | 93 | 66 | 69 | 76 | 87 | 77 | 82 | 85 | 88 |
90 | 88 | 67 | 88 | 91 | 96 | 68 | 97 | 59 | 88 |
整理、描述数据 :
按如下数据段整理、描述这两组数据
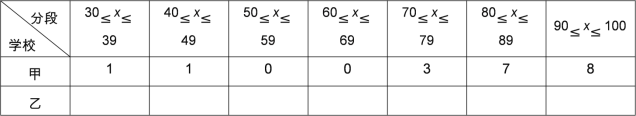
分析数据 :
两组数据的平均数、中位数、众数、方差如下表:

a经统计,表格中m的值是 ___________ .
得出结论:
b若甲学校有 400 名初二学生,估计这次考试成绩 80 分以上人数为____________ .
c可以推断出 _______学校学生的数学水平较高,理由为:①__________________;②_________________.(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,且
两点,且![]() ,
,![]() 两点均在直线
两点均在直线![]() 的下方,那么下列说法正确的是( )
的下方,那么下列说法正确的是( )
A.抛物线开口一定向上B.抛物线的顶点不可能在第四象限
C.抛物线与已知直线有两个交点D.抛物线的对称轴可能在![]() 轴右侧
轴右侧
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com