
【题目】甲、乙两人加工同一种零件,甲每天加工的数量是乙每天加工数量的 1.5 倍,两人各加工 600 个这种零件,甲比乙少用 5 天.
(1)求甲、乙两人每天各加工多少个这种零件?
(2)已知甲、乙两人加工这种零件每天的加工费分别是 150 元和 120 元,现有 3000 个这种零件的加工任务,甲单独加工一段时间后另有安排,剩余任务由乙单独完成.如果总加工费不超过 7800 元,那么甲至少加工了多少天?
【答案】(1)乙每天加工40个幂件,甲每天加工60个件;(2)甲至少加工40天.
【解析】
(1)设乙每天加工x个零件,则甲每天加工1.5x个零件,根据甲比乙少用5天,列分式方程求解;
(2)设甲加工了x天,乙加工了y天,根据3000个零件,列方程;根据总加工费不超过7800元,列不等式,方程和不等式综合考虑求解即可.
(1)设乙每天加工x个零件,则甲每天加工1.5x个零件
![]()
化简得600×1.5=600+5×1.5x
解得x=40
∴1.5x=60
经检验,x=40是分式方程的解且符合实际意义.
答:甲每天加工60个零件,乙每天加工,40个零件.
(2)设甲加工了x天,乙加工了y天,则由题意得
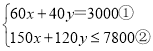
由①得y=75-1.5x ③
将③代入②得150x+120(75-1.5x)≤7800
解得x≥40,
当x=40时,y=15,符合问题的实际意义.
答:甲至少加工了40天.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C;把△BP2C绕点C顺时针旋转180°,得到△CP3D,依此类推,则旋转第2017次后,得到的等腰直角三角形的直角顶点P2018的坐标为( )
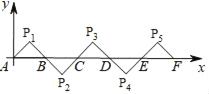
A. (4030,1) B. (4029,﹣1)
C. (4033,1) D. (4035,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高1元,其每天的销售量就减少20件.
(1)当售价定为12元时,每天可售出________件;
(2)要使每天利润达到640元,则每件售价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
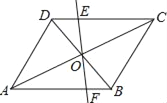
【题目】如图,点O是平行四边形ABCD的对称中心,将直线DB绕点O顺时针方向旋转,交DC、AB于点E、F.
(1)证明:△DEO≌△BFO;
(2)若DB=2,AD=1,AB=![]() ,当DB绕点O顺时针方向旋转45°时,判断四边形AECF的形状,并说明理由.
,当DB绕点O顺时针方向旋转45°时,判断四边形AECF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
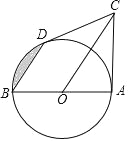
【题目】如图,AB是⊙O的直径,CD切⊙O于点D,且BD∥OC,连接AC.
(1)求证:AC是⊙O的切线;
(2)若AB=OC=4,求图中阴影部分的面积(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,过B作一直线与CD相交于点E,过A作AF垂直BE于点F,过C作CG垂直BE于点G,在FA上截取FH=FB,再过H作HP垂直AF交AB于P.若CG=3.则△CGE与四边形BFHP的面积之和为 _________ .
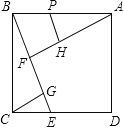
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,AB是⊙O的直径,OD⊥弦BC于点F,交⊙O于点E,连结CE、AE、CD,若∠AEC=∠ODC.
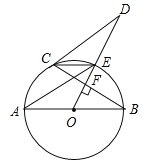
(1)求证:直线CD为⊙O的切线;
(2)若AB=5,BC=4,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(﹣ 2,﹣ 2),(![]() ,
,![]() ),…,都是梦之点,显然梦之点有无数个.
),…,都是梦之点,显然梦之点有无数个.
(1)若点 P(2,b)是反比例函数![]() (n 为常数,n ≠ 0) 的图象上的梦之点,求这个反比例函数解析式;
(n 为常数,n ≠ 0) 的图象上的梦之点,求这个反比例函数解析式;
(2)⊙O 的半径是![]() ,
,
①求出⊙O上的所有梦之点的坐标;
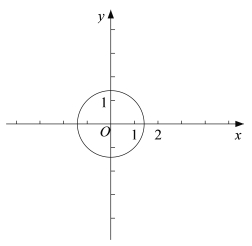
②已知点 M(m,3),点 Q 是(1)中反比例函数![]() 图象上异于点 P 的梦之点,过点Q 的直线 l 与 y 轴交于点 A,∠OAQ=45°.若在⊙ O 上存在一点 N,使得直线 MN ∥ l或 MN ⊥ l,求出 m 的取值范围.
图象上异于点 P 的梦之点,过点Q 的直线 l 与 y 轴交于点 A,∠OAQ=45°.若在⊙ O 上存在一点 N,使得直线 MN ∥ l或 MN ⊥ l,求出 m 的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com