
【题目】如图,已知![]() 是
是![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,过
,过![]() 的延长线上一点
的延长线上一点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,切点为点
,切点为点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() 是等腰三角形;
是等腰三角形;
(2)若![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
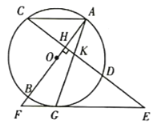
(1)如图1,连接OG.根据切线性质及CD⊥AB,可以推出∠KGE=∠AKH=∠GKE,根据等角对等边得到KE=GE,即可得到结果;
(2)AC与EF平行,理由为:如图2所示,连接GD,由∠KGE=∠GKE,及KG2=KDGE,利用两边对应成比例且夹角相等的两三角形相似可得出△GKD与△EKG相似,又利用同弧所对的圆周角相等得到∠C=∠AGD,可推知∠E=∠C,从而得到AC∥EF;
(3)如图3所示,连接OG,OC,先求出KE=GE,再求出圆的半径,根据勾股定理与垂径定理可以求解;然后在Rt△OGF中,解直角三角形即可求得FG的长度.
解:(1)证明:如图1,连接![]() ,
,
![]() 为
为![]() 的切线,
的切线,
![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴△EKG是等腰三角形;
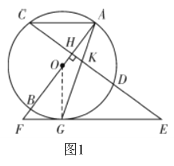
(2)证明:如图2,连接![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ;
;
![]()
(3)解:如图3,连接![]() ,
,![]() ,
,
由![]() ,可设
,可设![]() ,
,![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,根据勾股定理得
中,根据勾股定理得![]() ,
,
即![]() ,
,
解得![]() 或
或![]() (不合题意,舍去),
(不合题意,舍去),
![]() ,
,![]() ,
,
设![]() 的半径为
的半径为![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由勾股定理得![]() ,
,
即![]() ,
,
解得![]() ,
,
![]() 为
为![]() 的切线,
的切线,
![]() 为直角三角形,
为直角三角形,
在![]() 中,
中,![]() ,
,
![]() ,
,
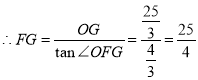 .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
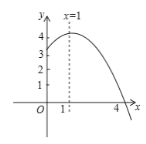
【题目】抛物线![]() (
(![]() )的部分图象如图所示,与
)的部分图象如图所示,与![]() 轴的一个交点坐标为
轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() ,下列结论是:①
,下列结论是:①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个不相等的实数根;④
有两个不相等的实数根;④![]() ;⑤若点
;⑤若点![]() 在该抛物线上,则
在该抛物线上,则![]() ,其中正确的个数有( )
,其中正确的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校是乒乓球体育传统项目校,为进一步推动该项目的发展.学校准备到体育用品店购买甲、乙两种型号乒乓球若干个,已知3个甲种乒乓球和5个乙种乒乓球共需50元,2个甲种乒乓球和3个乙种乒乓球共需31元.
(1)求1个甲种乒乓球和1个乙种乒乓球的售价各是多少元?
(2)学校准备购买这两种型号的乒乓球共200个,要求甲种乒乓球的数量不超过乙种乒乓球的数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
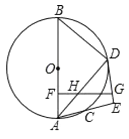
【题目】如图,已知![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,
上一点,![]() 的平分线交圆
的平分线交圆![]() 于点
于点![]() ,过
,过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,点
,点![]() 是
是![]() 中点,
中点,![]() ,
,![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,点
,点![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() 是等腰三角形;
是等腰三角形;
(3)若![]() ,求
,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是直角三角形,
是直角三角形,![]() .
.
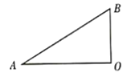
(1)请用尺规作图法,作![]() ,使它与
,使它与![]() 相切于点
相切于点![]() ,与
,与![]() 相交于点
相交于点![]() ;保留作图痕迹,不写作法,请标明字母)
;保留作图痕迹,不写作法,请标明字母)
(2)在(1)的图中,若![]() ,
,![]() ,求弧
,求弧![]() 的长.(结果保留
的长.(结果保留![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
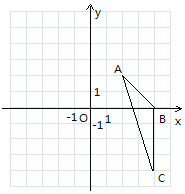
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(2,2),B(4,0),C(4,-4).
(1)请在图中画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在图中y轴右侧画出△A2B2C2,;
,得到△A2B2C2,请在图中y轴右侧画出△A2B2C2,;
(3)填空:△AA1A2的面积为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂对一批灯泡的质量进行随机抽查,见下表:
抽取灯泡数 | 40 | 100 | 150 | 500 | 1000 | 1500 |
优等品数 | 36 | 92 | 145 | 474 | 950 | 1427 |
优等品频率 |
(1)计算表中的优等品的频率(精确到0.001)
(2)根据抽査的灯泡优等品的频率,估计这批灯泡优等品的概率(精确到0.01)
查看答案和解析>>
科目:初中数学 来源: 题型:
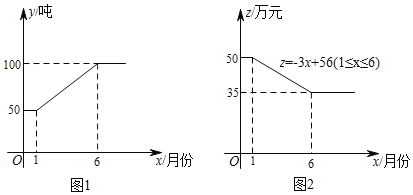
【题目】随着技术的发展进步,某公司2018年采用的新型原料生产产品.这种新型原料的用量y(吨)与月份x之间的关系如图1所示,每吨新型原料所生产的产品的售价z(万元)与月份x之间的关系如图2所示.已知将每吨这种新型原料加工成的产品的成本为20万元.
(1)求出该公司这种新型原料的用量y(吨)与月份x之间的函数关系式;
(2)若该公司利用新型原料所生产的产品当月都全部销售,求哪个月利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
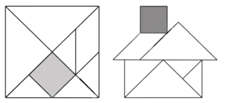
【题目】“七巧板”是我们祖先的一项卓越创造,可以拼出许多有趣的图形,被誉为“东方魔板”,图①是由边长![]() 的正方形薄板分成7块制作成的“七巧板”图②是用该“七巧板”拼成的一个“家”的图形,该“七巧板”中7块图形之一的正方形边长为_______
的正方形薄板分成7块制作成的“七巧板”图②是用该“七巧板”拼成的一个“家”的图形,该“七巧板”中7块图形之一的正方形边长为_______![]() (结果保留根号).
(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com