
【题目】研究发现,二次函数![]() (
(![]() )图象上任何一点到定点(0,
)图象上任何一点到定点(0,![]() )和到定直线
)和到定直线![]() 的距离相等.我们把定点(0,
的距离相等.我们把定点(0,![]() )叫做抛物线
)叫做抛物线![]() 的焦点,定直线
的焦点,定直线![]() 叫做抛物线
叫做抛物线![]() 的准线.
的准线.
(1)写出函数![]() 图象的焦点坐标和准线方程;
图象的焦点坐标和准线方程;
(2)等边三角形OAB的三个顶点都在二次函数![]() 图象上,O为坐标原点,求等边三角形的边长;
图象上,O为坐标原点,求等边三角形的边长;
(3)M为抛物线![]() 上的一个动点,F为抛物线
上的一个动点,F为抛物线![]() 的焦点,P(1,3)为定点,求MP+MF的最小值.
的焦点,P(1,3)为定点,求MP+MF的最小值.
【答案】(1)焦点坐标为:(0,1),准线方程为:y=-1;(2)8![]() ;(3)4.
;(3)4.
【解析】
(1)根据焦点坐标为(0,![]() ),准线方程为y=
),准线方程为y=![]() ,即可得出答案.
,即可得出答案.
(2)根据题意可设A(x,y),B(-x,y),从而根据等边三角形及抛物线的性质可得出∠AOE=30°,继而可得出![]() ,代入可得出x和y的值,也可求出等边三角形的边长.
,代入可得出x和y的值,也可求出等边三角形的边长.
(3)点P到点F的距离等于点P到准线的距离,从而根据垂线段最短的知识可找到点M的位置,结合图形可得出这个最小值.
解:(1)由题意得,焦点坐标为:(0,1),准线方程为:y=-1;
(2)设A(x,y),B(-x,y),
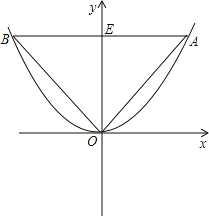
∵△OAB是等边三角形,
∴∠AOE=![]() ∠AOB=30°,
∠AOB=30°,
∴y=![]() x,
x,
将点A坐标(x,y)=(x,![]() x)代入函数解析式,可得
x)代入函数解析式,可得![]() x=
x=![]() x2,
x2,
解得:x=4![]() ,
,
故可得点A坐标为(4![]() ,12),三角形的边长=OA=
,12),三角形的边长=OA=![]() =8
=8![]() .
.
(3)过点M作MN⊥准线,交准线于点N,
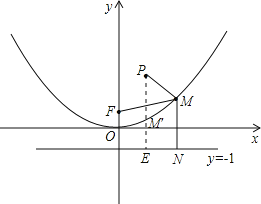
则由题意可得,MN=MF,
故可得:MP+MF=MP+MN,
结合图形可得过点P作PE⊥准线,交准线于点E,则PE与抛物线的交点M'能满足MP+MF最小,
此时M'P+M'F=PE=4.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】已知∠AOB,作图.
步骤1:在OB上任取一点M,以点M为圆心,MO长为半径画半圆,分别交OA、OB于点P、Q;
步骤2:过点M作PQ的垂线交 ![]() 于点C;
于点C;
步骤3:画射线OC.
则下列判断:①![]() =
=![]() ;②MC∥OA;③OP=PQ;④OC平分∠AOB,其中正确的个数为( )
;②MC∥OA;③OP=PQ;④OC平分∠AOB,其中正确的个数为( )
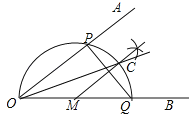
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两种糖果,原价分别为每千克a元和b元.根据调查,将两种糖果按甲种糖果x千克与乙种糖果y千克的比例混合,取得了较好的销售效果.现在糖果价格有了调整:甲种糖果单价下降15%,乙种糖果单价上涨20%,但按原比例混合的糖果单价恰好不变,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】日前,某公司决定对塘栖枇杷品种进行培育,育苗基地对其中的四个品种“白砂”“红袍”“夹脚”“宝珠”共500粒种子进行发芽试验,从中选择发芽率最高的品种进行推广,通过实验得知“白砂”品种的发芽率为![]() ,并把实验数据绘成两幅统计图(部分信息未给出):
,并把实验数据绘成两幅统计图(部分信息未给出):
![]()
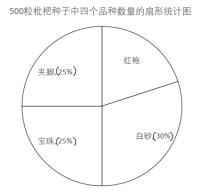
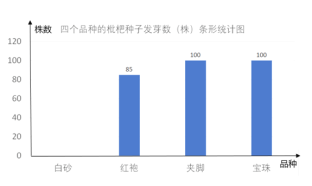
(1)求实验中“红袍”品种的种子数量;
(2)求实验中“白砂”品种的种子发芽的株数,并补全条形统计图;
(3)从以上信息,你认为应选哪一个品种进行推广,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
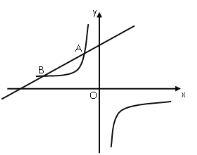
【题目】如图,一次函数![]() (
(![]() 为常数,且
为常数,且![]() )的图像与反比例函数
)的图像与反比例函数![]() 的图像交于
的图像交于![]() ,
,![]() 两点.
两点.
(1)求一次函数的表达式;
(2)若将直线![]() 向下平移
向下平移![]() 个单位长度后与反比例函数的图像有且只有一个公共点,求
个单位长度后与反比例函数的图像有且只有一个公共点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校举行“青春心向党建功新时代”演讲比赛活动,准备购买甲、乙两种奖品,小昆发现用480元购买甲种奖品的数目恰好与用360元购买乙种奖品的数目相等,已知甲种奖品的单价比乙种奖品的单价多10元.
(1)求甲、乙两种奖品的单价各是多少元?
(2)如果需要购买甲乙两种奖品共100个,且甲种奖品的数目不低于乙种奖品数目的2倍,问购买多少个甲种奖品,才使得总购买费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
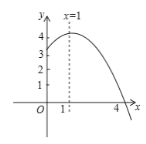
【题目】抛物线![]() (
(![]() )的部分图象如图所示,与
)的部分图象如图所示,与![]() 轴的一个交点坐标为
轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() ,下列结论是:①
,下列结论是:①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个不相等的实数根;④
有两个不相等的实数根;④![]() ;⑤若点
;⑤若点![]() 在该抛物线上,则
在该抛物线上,则![]() ,其中正确的个数有( )
,其中正确的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一条直线截三角形的两边,若所截得的四边形对角互补,则称该直线为三角形第三条边上的逆平行线.如图![]() ,
,![]() 为
为![]() 的截线,截得四边形
的截线,截得四边形![]() ,若
,若![]() ,则称
,则称![]() 为
为![]() 边
边![]() 的逆平行线;如图
的逆平行线;如图![]() ,已知
,已知![]() 中,
中,![]() ,过
,过![]() 边上的点
边上的点![]() 作
作![]() 交于点
交于点![]() ,过点
,过点![]() 作边
作边![]() 的逆平行线
的逆平行线![]() ,交
,交![]() 边于点
边于点![]() .
.
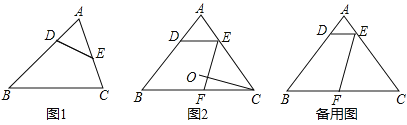
(1)求证:![]() 是边
是边![]() 的逆平行线.
的逆平行线.
(2)![]() 点是
点是![]() 的外心,连接
的外心,连接![]() ,求证:
,求证:![]() .
.
(3)已知![]() ,
,![]() ,过点
,过点![]() 作边
作边![]() 的逆平行线
的逆平行线![]() ,交边
,交边![]() 于点
于点![]() .
.
①试探索![]() 为何值时,四边形
为何值时,四边形![]() 的面积最大,并求出最大值;
的面积最大,并求出最大值;
②在①的条件下,比较![]()
![]() 大小关系.(“
大小关系.(“![]() 或
或![]() ”)
”)
查看答案和解析>>
科目:初中数学 来源: 题型:
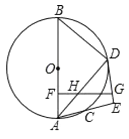
【题目】如图,已知![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,
上一点,![]() 的平分线交圆
的平分线交圆![]() 于点
于点![]() ,过
,过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,点
,点![]() 是
是![]() 中点,
中点,![]() ,
,![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,点
,点![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() 是等腰三角形;
是等腰三角形;
(3)若![]() ,求
,求![]() 的半径.
的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com