
【题目】解方程:
(1)用开平方法解方程:![]()
(2)用配方法解方程:x2 —4x+1=0
(3)用公式法解方程:3x2+5(2x+1)=0
(4)用因式分解法解方程:3(x-5)2=2(5-x)
(5)解方程:![]()
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中的点P和图形M,给出如下的定义:若在图形M存在一点Q,使得P、Q两点间的距离小于或等于1,则称P为图形M的关联点.
中的点P和图形M,给出如下的定义:若在图形M存在一点Q,使得P、Q两点间的距离小于或等于1,则称P为图形M的关联点.
(1)当⊙O的半径为2时,
①在点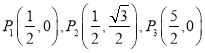 中,⊙O的关联点是_______________.
中,⊙O的关联点是_______________.
②点P在直线y=-x上,若P为⊙O 的关联点,求点P的横坐标的取值范围.
(2)⊙C 的圆心在x轴上,半径为2,直线y=-x+1与x轴、y轴交于点A、B.若线段AB上的所有点都是⊙C的关联点,直接写出圆心C的横坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一元二次方程![]() 满足
满足![]() ,那么我们称这个方程为“凤凰”方程.已知
,那么我们称这个方程为“凤凰”方程.已知![]() 是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=3,BC=4.以点C为圆心,r为半径的圆与边AB(边AB为线段)仅有一个公共点,则r的值为( )
A.r≥![]() B.r=3或r=4C.
B.r=3或r=4C.![]() ≤r≤4 D.r=
≤r≤4 D.r=![]() 或3<r≤4
或3<r≤4
查看答案和解析>>
科目:初中数学 来源: 题型:
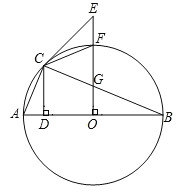
【题目】如图,△ACB内接于圆O,AB为直径,CD⊥AB与点D,E为圆外一点,EO⊥AB,与BC交于点G,与圆O交于点F,连接EC,且EG=EC.
(1)求证:EC是圆O的切线;
(2)当∠ABC=22.5°时,连接CF.
①求证:AC=CF;
②若AD=1,求线段FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 在以
在以![]() 为直径的半圆内.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
为直径的半圆内.请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
(1)在图1中作弦![]() ,使
,使![]() ;
;
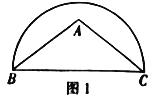
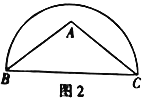
(2)在图2中以![]() 为边作一个45°的圆周角.
为边作一个45°的圆周角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天猫店销售某种规格学生软式排球,成本为每个30元.以往销售大数据分析表明:当每只售价为40元时,平均每月售出600个;若售价每上涨1元,其月销售量就减少20个,若售价每下降1元,其月销售量就增加200个.
(1)若售价上涨m元,每月能售出 个排球(用m的代数式表示).
(2)为迎接“双十一”,该天猫店在10月底备货1300个该规格的排球,并决定整个11月份进行降价促销,问售价定为多少元时,能使11月份这种规格排球获利恰好为8400元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.动点P从点A开始沿折线AC-CB-BA运动,点P在AC,CB,BA边上运动的速度分别为每秒3,4,5个单位.直线l从与AC重合的位置开始,以每秒![]() 个单位的速度沿CB方向移动,移动过程中保持l∥AC,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P第一次回到点A时,点P和直线l同时停止运动.
个单位的速度沿CB方向移动,移动过程中保持l∥AC,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P第一次回到点A时,点P和直线l同时停止运动.
(1)当t=5秒时,点P走过的路径长为_________;当t=_________秒时,点P与点E重合;
(2)当点P在AC边上运动时,连结PE,并过点E作AB的垂线,垂足为H. 若以C、P、E为顶点的三角形与△EFH相似,试求线段EH的值;
(3)当点P在折线AC-CB-BA上运动时,作点P关于直线EF的对称点Q.在运动过程中,若形成的四边形PEQF为菱形,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
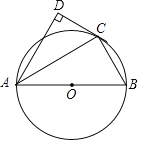
【题目】如图,AB为⊙O的直径,点D在⊙O外,∠BAD的平分线与⊙O交于点C,连接BC、CD,且∠D=90°.
(1)求证:CD是⊙O的切线;
(2)若∠DCA=60°,BC=3,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com