
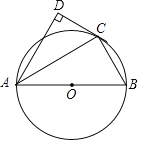
【题目】如图,AB为⊙O的直径,点D在⊙O外,∠BAD的平分线与⊙O交于点C,连接BC、CD,且∠D=90°.
(1)求证:CD是⊙O的切线;
(2)若∠DCA=60°,BC=3,求![]() 的长.
的长.
【答案】(1)见解析;(2)π
【解析】
(1)连接OC,只需证明∠OCD=90°即可;
(2)由圆周角定理得出∠ACB=90°,即可求得∠OCB=60°,得到△OBC是等边三角形,可求得半径为3,弧BC的圆心角度数,再利用弧长公式求得结果即可.
解:(1)证明:连接OC,
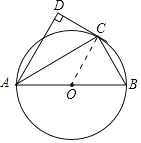
∵AC是∠BAD的平分线,
∴∠CAD=∠BAC,
又∵OA=OC,
∴∠OAC=∠OCA,
∴∠OCA=∠CAD,
∴OC∥AD,
∴∠OCD=∠D=90°,
∴CD是⊙O的切线;
(2)解:∵∠ACD=60°,
∴∠OCA=30°,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠OCB=60°,
∵OC=OB,
∴△OCB是等边三角形,
∴OB=OC=BC=3,∠COB=60°,
∴![]() 的长:
的长:![]() .
.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】解方程:
(1)用开平方法解方程:![]()
(2)用配方法解方程:x2 —4x+1=0
(3)用公式法解方程:3x2+5(2x+1)=0
(4)用因式分解法解方程:3(x-5)2=2(5-x)
(5)解方程:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校准备在教学楼后面搭建一个简易矩形自行车车棚,一边利用教学楼的后墙(可利用的墙长为19 m),另外三边利用学校现有总长38 m的铁栏围成.
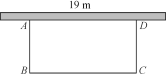
(1)若围成的面积为180 m2,试求出自行车车棚的长和宽;
(2)能围成面积为200 m2的自行车车棚吗?如果能,请你给出设计方,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,点P为△ABC内一点,∠APB=∠BAC=120°.若AP+BP=4,则PC的最小值为( )
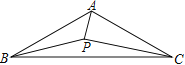
A. 2B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
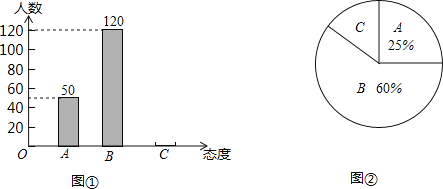
【题目】中学生骑电动车上学的现象越来越受到社会的关注.为此某媒体记者小李随机调查了城区若干名中学生家长对这种现象的态度(态度分为:A:无所谓;B:反对;C:赞成)并将调査结果绘制成图①和图②的统计图(不完整)请根据图中提供的信息,解答下列问题:
(1)此次抽样调査中.共调査了 名中学生家长;
(2)将图①补充完整;
(3)根据抽样调查结果.请你估计我市城区80000名中学生家长中有多少名家长持反对态度?
查看答案和解析>>
科目:初中数学 来源: 题型:
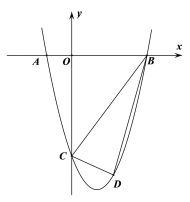
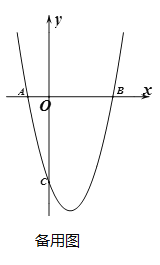
【题目】如图,在平面直角坐标系中抛物线![]() 交x轴于点A、B,交y轴于点C, A、B两点横坐标为-1和3,C点纵坐标为-4.
交x轴于点A、B,交y轴于点C, A、B两点横坐标为-1和3,C点纵坐标为-4.
(1)求抛物线的解析式;
(2)动点D在第四象限且在抛物线上,当△BCD面积最大时,求D点坐标,并求△BCD面积的最大值;
(3)抛物线的对称轴上是否存在一点Q,使得∠QBC=45°,如果存在,求出点Q的坐标,不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料
我们通过下列步骤估计方程2x2+x﹣2=0的根的所在的范围.
第一步:画出函数y=2x2+x﹣2的图象,发现图象是一条连续不断的曲线,且与x轴的一个
交点的横坐标在0,1之间.
第二步:因为当x=0时,y=﹣2<0;当x=1时,y=1>0.
所以可确定方程2x2+x﹣2=0的一个根x1所在的范围是0<x1<1.
第三步:通过取0和1的平均数缩小x1所在的范围;
取x=![]() ,因为当x=
,因为当x=![]() 时,y<0,
时,y<0,
又因为当x=1时,y>0,
所以![]() <x1<1.
<x1<1.
(1)请仿照第二步,通过运算,验证2x2+x﹣2=0的另一个根x2所在范围是﹣2<x2<﹣1;
(2)在﹣2<x2<﹣1的基础上,重复应用第三步中取平均数的方法,将x2所在范围缩小至m<x2<n,使得n﹣m≤![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx+c(a≠0)的图象于x轴的交点坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M(x0,y0)在x轴下方,对于以下说法:①b2﹣4ac>0②x=x0是方程ax2+bx+c=y0的解③x1<x0<x2④a(x0﹣x1)(x0﹣x2)<0其中正确的是( )
A.①③④B.①②④C.①②③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要证明平行四边形ABCD为正方形,那么我们需要在四边形ABCD是平行四边形的基础上,进一步证明( )
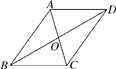
A.AB=AD且AC⊥BDB.AB=AD且AC=BDC.∠A=∠B且AC=BDD.AC和BD互相垂直平分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com