
【题目】阅读下列材料
我们通过下列步骤估计方程2x2+x﹣2=0的根的所在的范围.
第一步:画出函数y=2x2+x﹣2的图象,发现图象是一条连续不断的曲线,且与x轴的一个
交点的横坐标在0,1之间.
第二步:因为当x=0时,y=﹣2<0;当x=1时,y=1>0.
所以可确定方程2x2+x﹣2=0的一个根x1所在的范围是0<x1<1.
第三步:通过取0和1的平均数缩小x1所在的范围;
取x=![]() ,因为当x=
,因为当x=![]() 时,y<0,
时,y<0,
又因为当x=1时,y>0,
所以![]() <x1<1.
<x1<1.
(1)请仿照第二步,通过运算,验证2x2+x﹣2=0的另一个根x2所在范围是﹣2<x2<﹣1;
(2)在﹣2<x2<﹣1的基础上,重复应用第三步中取平均数的方法,将x2所在范围缩小至m<x2<n,使得n﹣m≤![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】
(1)计算x=﹣2和x=﹣1时,y的值,确定其x2所在范围是﹣2<x2<﹣1;
(2)先根据第三步﹣2和﹣1的平均数确定x=﹣![]() ,计算x=﹣
,计算x=﹣![]() 时y的值,得﹣
时y的值,得﹣![]() <x2<﹣1,同理再求﹣1和﹣
<x2<﹣1,同理再求﹣1和﹣![]() 的平均数为﹣
的平均数为﹣![]() ,计算x=﹣
,计算x=﹣![]() 时y的值,从而得结论.
时y的值,从而得结论.
(1)解:因为当x=﹣2时,y>0;当x=﹣1时,y<0,
所以方程2x2+x﹣2=0的另一个根x2所在的范围是﹣2<x2<﹣1.…
(2)取x=![]() =﹣
=﹣![]() ,因为当x=﹣
,因为当x=﹣![]() 时,y=2×
时,y=2×![]() ﹣
﹣![]() ﹣2=1>0,
﹣2=1>0,
又因为当x=﹣1时,y=﹣1<0,
所以﹣![]() <x2<﹣1,
<x2<﹣1,
取x= =﹣
=﹣![]() ,因为当x=﹣
,因为当x=﹣![]() 时,y=2×
时,y=2×![]() ﹣
﹣![]() ﹣2=﹣
﹣2=﹣![]() <0,
<0,
又因为当x=﹣![]() 时,y>0,
时,y>0,
所以﹣![]() <x2<﹣
<x2<﹣![]() ,
,
又因为﹣![]() ﹣(﹣
﹣(﹣![]() )=
)=![]() ,
,
所以﹣![]() <x2<﹣
<x2<﹣![]() 即为所求x2 的范围.
即为所求x2 的范围.



科目:初中数学 来源: 题型:
【题目】某天猫店销售某种规格学生软式排球,成本为每个30元.以往销售大数据分析表明:当每只售价为40元时,平均每月售出600个;若售价每上涨1元,其月销售量就减少20个,若售价每下降1元,其月销售量就增加200个.
(1)若售价上涨m元,每月能售出 个排球(用m的代数式表示).
(2)为迎接“双十一”,该天猫店在10月底备货1300个该规格的排球,并决定整个11月份进行降价促销,问售价定为多少元时,能使11月份这种规格排球获利恰好为8400元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,把矩形OCBA绕点C顺时针旋转α角,得到矩形FCDE,设FC与AB交于点H,且A(0,4),C(6,0).
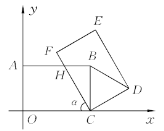
(1)当α=45°时,求H点的坐标.
(2)当α=60°时,ΔCBD是什么特殊的三角形?说明理由.
(3)当AH=HC时,求直线HC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
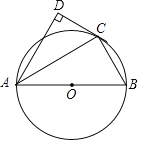
【题目】如图,AB为⊙O的直径,点D在⊙O外,∠BAD的平分线与⊙O交于点C,连接BC、CD,且∠D=90°.
(1)求证:CD是⊙O的切线;
(2)若∠DCA=60°,BC=3,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=|a|x2+bx+c的图象经过A(m,n)、B(0,y1)、C(3-m,n)、D(![]() , y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
, y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
A. y1< y2< y3B. y1 < y3< y2C. y3< y2< y1D. y2< y3< y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小芳做一个“配色”的游戏.右图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色.同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,或者转盘A转出了蓝色,转盘B转出了红色,则红色和蓝色在一起配成紫色,这种情况下小芳获胜;同样,蓝色和黄色在一起配成绿色,这种情况下小明获胜;在其它情况下,则小明、小芳不分胜负.
(1)利用列表或树状图的方法表示此游戏所有可能出现的结果;
(2)此游戏的规则,对小明、小芳公平吗?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
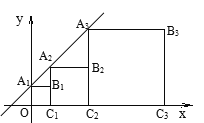
【题目】如图,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线![]() (k>0)和x轴上,已知点B1(1,1),B2(3,2),则Bn的坐标是__________________.
(k>0)和x轴上,已知点B1(1,1),B2(3,2),则Bn的坐标是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
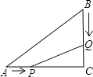
【题目】如图,△ABC中,∠C=90,AB=10cm,AC=8cm,点P从点A开始出发向点C以2cm/s的速度移动,点Q从B点出发向点C以1cm/s的速度移动,若P、Q分别同时从A,B出发,几秒后四边形APQB是△ABC面积的![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.

(1)求点C的坐标及抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,求点D的坐标;并直接写出直线BC、直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD,若存在,请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com